粘度随压力变化的流体沿斜面向下流动：长波线性稳定性分析

IF 2.8 3区工程技术 Q2 MECHANICS

International Journal of Non-Linear Mechanics Pub Date : 2024-10-28 DOI:10.1016/j.ijnonlinmec.2024.104930

Benedetta Calusi

{"title":"粘度随压力变化的流体沿斜面向下流动：长波线性稳定性分析","authors":"Benedetta Calusi","doi":"10.1016/j.ijnonlinmec.2024.104930","DOIUrl":null,"url":null,"abstract":"<div><div>In this paper, we investigate the linear stability of a gravity-driven fluid with pressure-dependent viscosity flowing down an inclined plane. The linear stability analysis is formulated using the long-wave approximation method. We show that the onset of instability occurs at a critical Reynolds number that depends on the material and geometrical parameters. Our results suggest that the dependence of the viscosity on pressure can influence the stability characteristics of the flow down an incline.</div></div>","PeriodicalId":50303,"journal":{"name":"International Journal of Non-Linear Mechanics","volume":"168 ","pages":"Article 104930"},"PeriodicalIF":2.8000,"publicationDate":"2024-10-28","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Flow of fluids with pressure-dependent viscosity down an incline: Long-wave linear stability analysis\",\"authors\":\"Benedetta Calusi\",\"doi\":\"10.1016/j.ijnonlinmec.2024.104930\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><div>In this paper, we investigate the linear stability of a gravity-driven fluid with pressure-dependent viscosity flowing down an inclined plane. The linear stability analysis is formulated using the long-wave approximation method. We show that the onset of instability occurs at a critical Reynolds number that depends on the material and geometrical parameters. Our results suggest that the dependence of the viscosity on pressure can influence the stability characteristics of the flow down an incline.</div></div>\",\"PeriodicalId\":50303,\"journal\":{\"name\":\"International Journal of Non-Linear Mechanics\",\"volume\":\"168 \",\"pages\":\"Article 104930\"},\"PeriodicalIF\":2.8000,\"publicationDate\":\"2024-10-28\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"International Journal of Non-Linear Mechanics\",\"FirstCategoryId\":\"5\",\"ListUrlMain\":\"https://www.sciencedirect.com/science/article/pii/S0020746224002956\",\"RegionNum\":3,\"RegionCategory\":\"工程技术\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MECHANICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"International Journal of Non-Linear Mechanics","FirstCategoryId":"5","ListUrlMain":"https://www.sciencedirect.com/science/article/pii/S0020746224002956","RegionNum":3,"RegionCategory":"工程技术","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MECHANICS","Score":null,"Total":0}

引用次数: 0

摘要

本文研究了流体在重力驱动下的线性稳定性，该流体的粘度与压力有关。线性稳定性分析采用长波近似法。结果表明，不稳定性发生在一个临界雷诺数上，而这个临界雷诺数取决于材料和几何参数。我们的结果表明，粘度对压力的依赖会影响斜面下流动的稳定性特征。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

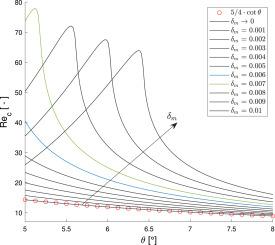
Flow of fluids with pressure-dependent viscosity down an incline: Long-wave linear stability analysis

查看原文本刊更多论文

Flow of fluids with pressure-dependent viscosity down an incline: Long-wave linear stability analysis

In this paper, we investigate the linear stability of a gravity-driven fluid with pressure-dependent viscosity flowing down an inclined plane. The linear stability analysis is formulated using the long-wave approximation method. We show that the onset of instability occurs at a critical Reynolds number that depends on the material and geometrical parameters. Our results suggest that the dependence of the viscosity on pressure can influence the stability characteristics of the flow down an incline.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

International Journal of Non-Linear Mechanics 物理-力学

CiteScore

5.50

自引率

9.40%

发文量

192

审稿时长

67 days

期刊介绍： The International Journal of Non-Linear Mechanics provides a specific medium for dissemination of high-quality research results in the various areas of theoretical, applied, and experimental mechanics of solids, fluids, structures, and systems where the phenomena are inherently non-linear. The journal brings together original results in non-linear problems in elasticity, plasticity, dynamics, vibrations, wave-propagation, rheology, fluid-structure interaction systems, stability, biomechanics, micro- and nano-structures, materials, metamaterials, and in other diverse areas. Papers may be analytical, computational or experimental in nature. Treatments of non-linear differential equations wherein solutions and properties of solutions are emphasized but physical aspects are not adequately relevant, will not be considered for possible publication. Both deterministic and stochastic approaches are fostered. Contributions pertaining to both established and emerging fields are encouraged.