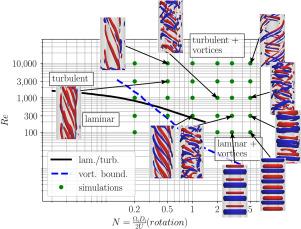
Turbulent spiral flow of power-law fluid in annular channel

Transient three-dimensional numerical simulations of power-law fluid flow in an annular channel with a diameter ratio of 1/2 were performed. The outcomes of the simulations using the URANS approach were contrasted with the results of the RANS and LES approaches for Newtonian and power-law fluids. It was demonstrated that comparable outcomes to those obtained through LES can be achieved through URANS with a reduced computational cost. It was determined that the RANS approach tends to underestimate turbulent kinetic energy and pressure losses. Parametric studies were conducted using the URANS approach, encompassing a range of Reynolds numbers ($Re$) between 100 and 10,000, dimensionless rotation rates ($N$) values between 0.2 and 5, and power-law indices ($n$) between 0.4 and 1. The following flow regimes were identified: (1) flow without vortices; (2) Taylor-type toroidal vortices; (3) Görtler-type continuous spiral vortices swirling around the inner cylinder; and (4) small-scale Görtler-type vortices near both channel walls. The numerical experiments demonstrated that the rotation of the inner cylinder resulted in three notable effects: a reduction in the apparent viscosity within the vicinity of the rotating cylinder, a decline in viscous shear stresses, and the development of Görtler-type vortex structures, which contributed to an increase in energy losses. Additionally, at Reynolds numbers below 300, high rotation led to the formation of Taylor-type vortices and a reduction in pressure losses. The power law fluid requires increased rotation of the inner cylinder to form vortices and transition the flow to turbulent. When the Reynolds number is less than 300, the first mechanism is the dominant factor, resulting in a reduction in pressure loss. At Reynolds numbers of approximately 300, the first two mechanisms are in competition, with the pressure loss dependent on the power law index, $n$. Finally, at Reynolds numbers greater than 300, secondary vortex structures, such as Görtler vortices, become the dominant factor, leading to an increase in pressure loss with rotation.