环状嵌段共聚物熔体的密度泛函理论
IF 5.1
1区 化学
Q1 POLYMER SCIENCE
引用次数: 0
摘要
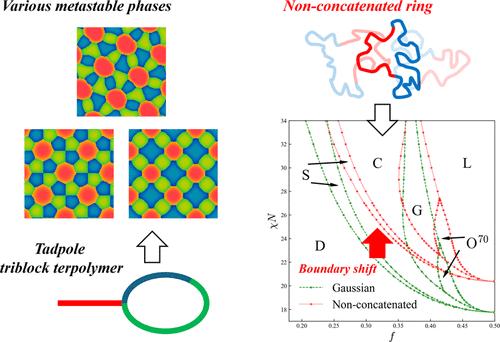
我们提出了一种基于金兹堡-朗道(Ginzburg-Landau)型密度泛函理论并结合随机相近似的高效方法,用于在熔体中自组装具有一般环状结构的高斯嵌段共聚物和非嵌段环状嵌段共聚物。对于高斯共聚物,密度泛函理论的适用性通过图拉普拉卡的高斯嵌入方法得到了增强,该方法可以评估包括内部多循环在内的任意结构的单链散射函数,而不存在分析上的困难。利用这种方法,我们以与线性二嵌段共聚物相同的成本预测了环状和自行车状二嵌段共聚物的相图,并发现了蝌蚪状三嵌段三元共聚物的各种蜕变形态,而线性和星形三嵌段三元共聚物尚未观察到这些形态。我们还证明,我们的框架可以借助实验获得的单链散射函数预测非缩合环状二嵌段共聚物的相图。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Density Functional Theory for Cyclic Block Copolymer Melts
We propose an efficient method for the self-assembly of Gaussian block copolymers with general cyclic architectures and nonconcatenated ring block copolymer in a melt based on a Ginzburg–Landau-type density functional theory combined with random phase approximation. For the Gaussian copolymers, the applicability of the density functional theory is enhanced by a Gaussian embedding method with a graph Laplacian, which allows evaluating single-chain scattering functions for arbitrary architectures including internal multicycles without analytical difficulty. By using this methodology, we predict phase diagrams of ring and bicycle diblock copolymers at the same cost as a linear diblock copolymer, and discover various metastable morphologies of a tadpole triblock terpolymer, which have not been observed for linear and star triblock terpolymers. We also demonstrate that our framework predicts the phase diagram of the nonconcatenated ring diblock copolymer with the aid of its single-chain scattering function obtained by experiments.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Macromolecules
工程技术-高分子科学
CiteScore
9.30
自引率
16.40%
发文量
942
审稿时长
2 months
期刊介绍:
Macromolecules publishes original, fundamental, and impactful research on all aspects of polymer science. Topics of interest include synthesis (e.g., controlled polymerizations, polymerization catalysis, post polymerization modification, new monomer structures and polymer architectures, and polymerization mechanisms/kinetics analysis); phase behavior, thermodynamics, dynamic, and ordering/disordering phenomena (e.g., self-assembly, gelation, crystallization, solution/melt/solid-state characteristics); structure and properties (e.g., mechanical and rheological properties, surface/interfacial characteristics, electronic and transport properties); new state of the art characterization (e.g., spectroscopy, scattering, microscopy, rheology), simulation (e.g., Monte Carlo, molecular dynamics, multi-scale/coarse-grained modeling), and theoretical methods. Renewable/sustainable polymers, polymer networks, responsive polymers, electro-, magneto- and opto-active macromolecules, inorganic polymers, charge-transporting polymers (ion-containing, semiconducting, and conducting), nanostructured polymers, and polymer composites are also of interest. Typical papers published in Macromolecules showcase important and innovative concepts, experimental methods/observations, and theoretical/computational approaches that demonstrate a fundamental advance in the understanding of polymers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


