几乎不受约束的非线性多输入多输出(MIMO)跟踪控制系统 LMI 的低复杂度解决方案
IF 3.7
3区 计算机科学
Q2 AUTOMATION & CONTROL SYSTEMS
Journal of The Franklin Institute-engineering and Applied Mathematics
Pub Date : 2024-10-25
DOI:10.1016/j.jfranklin.2024.107350
引用次数: 0
摘要
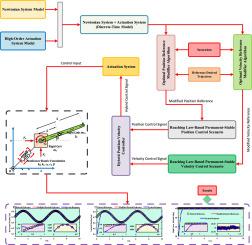
本研究致力于非线性多输入多输出(MIMO)牛顿力学系统的离散时间跟踪控制,该系统具有相等数量的输入和输出,且存在输入饱和和执行系统的高阶动态。首先,利用 Adams-Bashforth 和 Adams-Moulton 离散化技术将工厂和执行系统的连续时间模型转换为离散时间域。下一步,考虑到饱和边界,使用基于离散时间达成律的控制方法,得出修正后的位置和速度参考值。这些修改后的参考值通过优化算法获得,该算法可计算出与所需参考轨迹最接近的可实现位置和速度轨迹。在多输入多输出系统中修改所需的轨迹会形成一个线性矩阵不等式(LMI)系统。解决这种不等式系统需要使用复杂的方法,而且随着系统自由度(DOFs)的增加,难度也会增加。所提出的策略为解决这些不等式提供了一种更直接的方法。计算出修改后的参考点后,就可以使用上述达到律策略获得相应的位置和速度控制信号。建议算法的最后一步是使用高斯加权平均法将得到的位置和速度控制信号组合起来,形成主控制信号。通过适当调整高斯权重函数的标准偏差,控制系统可以获得理想的性能。为了评估所提出方法的性能特点,我们将其应用于一个非线性三维空间机械系统的跟踪控制程序中。数值模拟结果证明了该方法的有效性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
A low-complexity solution for LMIs of hardly constrained nonlinear MIMO tracking control systems
This research is dedicated to the discrete-time tracking control of nonlinear multi-input multi-output (MIMO) Newtonian mechanics systems with an equal number of inputs and outputs, in the presence of input saturation and high-order dynamics of the actuation system. Firstly, the continuous-time model of the plant and actuation system has been transformed into the discrete-time domain using Adams–Bashforth and Adams–Moulton discretization techniques. In the next step, considering saturation boundaries, the modified position and velocity references are derived using the discrete-time reaching law-based control approach. These modified references are obtained through an optimization algorithm that calculates the closest achievable position and velocity trajectories with respect to the desired reference trajectory. Modifying desired trajectories in MIMO systems results in the formation of a system of linear matrix inequalities (LMIs). Solving such systems of inequalities requires the use of complex methods, and this difficulty increases with the increase in the system’s degrees of freedom (DOFs). The proposed strategy offers a more straightforward approach to solving these inequalities. Once the modified references are calculated, the corresponding position and velocity control signals can be obtained using the mentioned reaching law strategies. The final step of the proposed algorithm is to combine the resulting position and velocity control signals using a Gaussian-weighted averaging method to form the main control signal. A desirable performance for the control system can be achieved by appropriately adjusting the standard deviations of the Gaussian weighing functions. To evaluate the performance characteristics of the proposed method, it has been applied in the tracking control procedure of a nonlinear 3-DOF mechanical system. The numerical simulation results demonstrate the effectiveness of the method.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
7.30
自引率
14.60%
发文量
586
审稿时长
6.9 months
期刊介绍:
The Journal of The Franklin Institute has an established reputation for publishing high-quality papers in the field of engineering and applied mathematics. Its current focus is on control systems, complex networks and dynamic systems, signal processing and communications and their applications. All submitted papers are peer-reviewed. The Journal will publish original research papers and research review papers of substance. Papers and special focus issues are judged upon possible lasting value, which has been and continues to be the strength of the Journal of The Franklin Institute.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


