最大恢复力的标准偏差控制着面心立方多元素合金的内在强度
IF 8.3
1区 材料科学
Q1 MATERIALS SCIENCE, MULTIDISCIPLINARY
引用次数: 0
摘要
在本研究中,我们采用多层面方法探索了面心立方多元素合金 (FCC) 固有强度的内在机理。我们的方法综合了原子模拟、内嵌原子模型和神经网络势能、第一原理计算、随机 Peierls-Nabarro (PN) 建模和符号机器学习。我们发现,在各种电位中,MPEA 的强度与最大叠加故障恢复力的标准偏差(τmax,sd)之间存在一致、稳健的线性相关关系。通过比较康托尔合金子系统和 Ni62.5V37.5 的实验强度与高通量第一原理计算得出的 τmax,sd 值,这一发现得到了证实。我们的理论见解来自于将随机 Peierls-Nabarro 模型与可剪切沉淀硬化框架相结合,证明了仅靠晶格畸变并不能直接提高固有强度。相反,τmax,sd 是一个关键的决定因素,能够将 MPEA 的强度提高多达十倍。我们的分析揭示了 PN 模型指数形式的关键作用,它通过将 τmax 的高斯分布转化为局部 Peierls 应力的指数分布,实现了强度的大幅提高。此外,利用先进的符号机器学习技术--确定独立性筛选和稀疏化算子(SISSO)方法,我们得出了 MPEA 强度、弹性特性和 τmax 统计量之间的可解释关系,为先进 MPEA 的设计和优化提供了新的见解。这些发现突出表明,MPEA 的非线性物理特性和原子波动不仅是其非常规内在强度的基础,而且还有助于形成其他复杂特性,如缓慢扩散和鸡尾酒效应。本文章由计算机程序翻译,如有差异,请以英文原文为准。
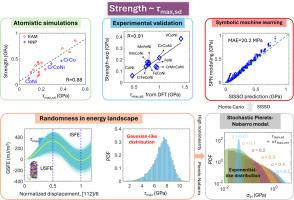
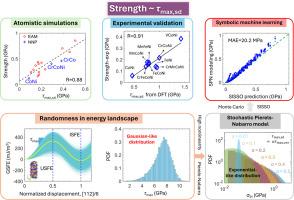
Standard deviation in maximum restoring force controls the intrinsic strength of face-centered cubic multi-principal element alloys
In this study, we explore the mechanisms underlying the exceptional intrinsic strength of face-centered cubic (FCC) Multi-Principal Element Alloys (MPEAs) using a multifaceted approach. Our methods integrate atomistic simulations, informed by both embedded-atom model and neural network potentials, with first-principles calculations, stochastic Peierls-Nabarro (PN) modeling, and symbolic machine learning. We identify a consistent, robust linear correlation between the strength of MPEAs and the standard deviation of the maximum stacking-fault restoring force (τmax,sd) across various potentials. This finding is substantiated by comparing the experimental strengths of Cantor alloys’ subsystems and Ni62.5V37.5 against τmax,sd values from high-throughput first-principle calculations. Our theoretical insights are derived from integrating the stochastic Peierls-Nabarro model with a shearable precipitation hardening framework, demonstrating that lattice distortion alone does not directly enhance intrinsic strength. Instead, τmax,sd emerges as a critical determinant, capable of boosting the strength of MPEAs by up to tenfold. Our analysis reveals the critical role of the exponential form of the PN model in achieving substantial strength improvement by transforming the Gaussian-like distribution of τmax into an exponential-like distribution of local Peierls stress. Additionally, using an advanced symbolic machine learning technique, the sure independence screening and sparsifying operator (SISSO) method, we derive interpretable relationships between MPEA strength, elastic properties, and τmax statistics, offering new insights into the design and optimization of advanced MPEAs. These findings highlight that the nonlinear physics and atomic fluctuations characterizing MPEAs not only underpin their unconventional intrinsic strength but also contribute to other complex properties such as sluggish diffusion and cocktail effect.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Acta Materialia
工程技术-材料科学:综合
CiteScore
16.10
自引率
8.50%
发文量
801
审稿时长
53 days
期刊介绍:
Acta Materialia serves as a platform for publishing full-length, original papers and commissioned overviews that contribute to a profound understanding of the correlation between the processing, structure, and properties of inorganic materials. The journal seeks papers with high impact potential or those that significantly propel the field forward. The scope includes the atomic and molecular arrangements, chemical and electronic structures, and microstructure of materials, focusing on their mechanical or functional behavior across all length scales, including nanostructures.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


