非线性固体力学的准无网格方法:域离散化与解法离散化的分离
IF 6.9
1区 工程技术
Q1 ENGINEERING, MULTIDISCIPLINARY
Computer Methods in Applied Mechanics and Engineering
Pub Date : 2024-10-23
DOI:10.1016/j.cma.2024.117459
引用次数: 0
摘要
在许多应用中,所关注的领域几何形状复杂,包含许多小特征。这些特征通常需要手动去除,以方便传统的基于元素的网格划分过程。这种手动去除过程取决于仿真目标,通常涉及主观的启发式方法。为了提供一种独立于领域离散化的灵活且易于调整的控制方程离散化过程,我们提出了一种无元素 Galerkin 方法,其中首先使用细尺度三角剖分对全特征领域进行离散化,然后使用粗尺度无元素离散化来近似求解控制方程。由于不是直接用于近似求导方程的解,因此细尺度三角剖分的质量可能很差,而且非常精细。粗尺度无元素基础具有局部支持,可通过细化或粗化进行调整,而无需改变细尺度三角剖分或其他几何考虑。无元素基函数使用传统的移动最小二乘法程序构建,但初始权重函数使用流形大地线构建,可普遍适用于非凸域。利用二级粗尺度无元素基础和梯度投影技术对治理方程的弱形式进行积分。梯度投影方法确保了必要的一致性,从而通过了补丁测试并获得了最佳收敛率。由于同时使用了无网格和基于网格的概念,整个方法被称为准无网格方法。为了演示整个方法,介绍了几个验证问题和非线性应用实例。本文章由计算机程序翻译,如有差异,请以英文原文为准。
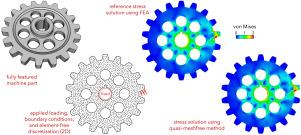
A quasi-meshfree method for nonlinear solid mechanics: Separating domain discretization from solution discretization
In many applications, domains of interest are geometrically complex containing numerous small features. These features are typically removed in a manual process to facilitate a conventional element-based meshing process. This manual defeaturing process is dependent upon the goals of the simulation and typically involves subjective heuristics. To provide a flexible and easily adaptable discretization process of the governing equations that is independent of the domain discretization, an element-free Galerkin method is proposed in which a fine-scale triangulation is used to first discretize the fully featured domain, but then a coarse-scale element-free discretization is used to approximate the solution of the governing equations. The fine-scale triangulation can be of poor quality and extremely refined since it is not used directly to approximate the solution of the governing equations. The coarse-scale element-free basis has local support and can be adapted through refinement or coarsening without the need to alter the fine-scale triangulation or other geometric considerations. The element-free basis functions are constructed using a conventional moving-least-squares procedure, but the initial weight functions are constructed using manifold geodesics for general applicability to non-convex domains. The weak form of the governing equations is integrated using a secondary coarse-scale element-free basis and a gradient projection technique. The projected-gradient methodology ensures the necessary consistency properties to pass the patch test and obtain optimal rates of convergence. The overall method is termed quasi-meshfree since both meshfree and mesh-based concepts are used. Several verification problems and nonlinear application examples are presented to demonstrate the overall method.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
12.70
自引率
15.30%
发文量
719
审稿时长
44 days
期刊介绍:
Computer Methods in Applied Mechanics and Engineering stands as a cornerstone in the realm of computational science and engineering. With a history spanning over five decades, the journal has been a key platform for disseminating papers on advanced mathematical modeling and numerical solutions. Interdisciplinary in nature, these contributions encompass mechanics, mathematics, computer science, and various scientific disciplines. The journal welcomes a broad range of computational methods addressing the simulation, analysis, and design of complex physical problems, making it a vital resource for researchers in the field.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


