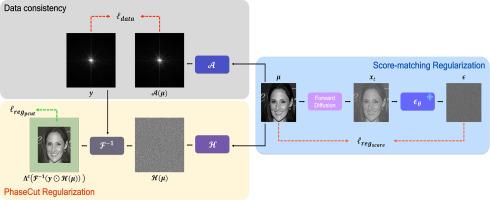
Regularization by denoising diffusion process meets deep relaxation in phase

Fourier phase retrieval is one of the representative inverse problems where a signal needs to be recovered using only the measured magnitude of its Fourier transform. Deep learning-based algorithms for solving Fourier phase retrieval have been widely studied. These methods provide better reconstruction than the conventional algorithms, such as alternating projection approaches and convex relaxation methods. However, it is difficult to recover the phase information of 256 × 256 images accurately, and they often cannot provide fine details and textures. Recently, diffusion models have been used to solve Fourier phase retrieval problems. They offer realistic reconstruction results, but due to the nature of generative models, they often create non-existent features in the actual images. To address these issues, we introduced a novel algorithm inspired by regularization by denoising diffusion, a variational diffusion sampling for reconstructing the images from the measurements. In particular, the optimization problem in the convex relaxation approach for phase retrieval is interpreted as an additional constraint during the variational sampling process to estimate the phase from the given Fourier magnitude measurement. The proposed method stands out by leveraging not only pre-trained diffusion models as image priors but also the classical optimization approach as the regularization. This novel combination ensures not just accurate phase reconstruction, but also performance guarantees. Our experiments demonstrate that the proposed algorithm consistently provides state-of-the-art performance across various datasets of 256 × 256 images. We further showed the effectiveness of the new regularization for the performance gain in the phase estimation.