结构单调夹杂的原点-双向后向反射前向分裂算法

IF 0.3 Q4 MATHEMATICS

Acta Mathematica Vietnamica Pub Date : 2024-06-28 DOI:10.1007/s40306-024-00535-7

Vũ Công Bằng, Dimitri Papadimitriou, Vũ Xuân Nhâm

{"title":"结构单调夹杂的原点-双向后向反射前向分裂算法","authors":"Vũ Công Bằng, Dimitri Papadimitriou, Vũ Xuân Nhâm","doi":"10.1007/s40306-024-00535-7","DOIUrl":null,"url":null,"abstract":"<div><p>We propose a primal-dual backward reflected forward splitting method for solving structured primal-dual monotone inclusions in real Hilbert spaces. The algorithm allows to use the inexact computations of Lipschitzian and cocoercive operators. The strong convergence of the generated iterative sequence is proved under the strong monotonicity condition, whilst the weak convergence is formally proved under several conditions used in the literature. An application to a structured minimization problem is provided.</p></div>","PeriodicalId":45527,"journal":{"name":"Acta Mathematica Vietnamica","volume":null,"pages":null},"PeriodicalIF":0.3000,"publicationDate":"2024-06-28","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"A Primal-dual Backward Reflected Forward Splitting Algorithm for Structured Monotone Inclusions\",\"authors\":\"Vũ Công Bằng, Dimitri Papadimitriou, Vũ Xuân Nhâm\",\"doi\":\"10.1007/s40306-024-00535-7\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div><p>We propose a primal-dual backward reflected forward splitting method for solving structured primal-dual monotone inclusions in real Hilbert spaces. The algorithm allows to use the inexact computations of Lipschitzian and cocoercive operators. The strong convergence of the generated iterative sequence is proved under the strong monotonicity condition, whilst the weak convergence is formally proved under several conditions used in the literature. An application to a structured minimization problem is provided.</p></div>\",\"PeriodicalId\":45527,\"journal\":{\"name\":\"Acta Mathematica Vietnamica\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.3000,\"publicationDate\":\"2024-06-28\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Acta Mathematica Vietnamica\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s40306-024-00535-7\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Acta Mathematica Vietnamica","FirstCategoryId":"1085","ListUrlMain":"https://link.springer.com/article/10.1007/s40306-024-00535-7","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们提出了一种求解实希尔伯特空间中结构化原始双单调夹杂的原始双向后向反射前向分裂方法。该算法允许使用 Lipschitzian 和 cocoercive 算子的非精确计算。在强单调性条件下证明了生成的迭代序列的强收敛性，而在文献中使用的几个条件下正式证明了弱收敛性。研究还提供了结构最小化问题的应用。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

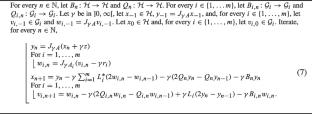
A Primal-dual Backward Reflected Forward Splitting Algorithm for Structured Monotone Inclusions

We propose a primal-dual backward reflected forward splitting method for solving structured primal-dual monotone inclusions in real Hilbert spaces. The algorithm allows to use the inexact computations of Lipschitzian and cocoercive operators. The strong convergence of the generated iterative sequence is proved under the strong monotonicity condition, whilst the weak convergence is formally proved under several conditions used in the literature. An application to a structured minimization problem is provided.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Acta Mathematica Vietnamica MATHEMATICS-

CiteScore

0.90

自引率

0.00%

发文量

期刊介绍： Acta Mathematica Vietnamica is a peer-reviewed mathematical journal. The journal publishes original papers of high quality in all branches of Mathematics with strong focus on Algebraic Geometry and Commutative Algebra, Algebraic Topology, Complex Analysis, Dynamical Systems, Optimization and Partial Differential Equations.