通过遍历功能不变路径来设计灵活的机器学习系统
IF 18.8
1区 计算机科学
Q1 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE
引用次数: 0
摘要
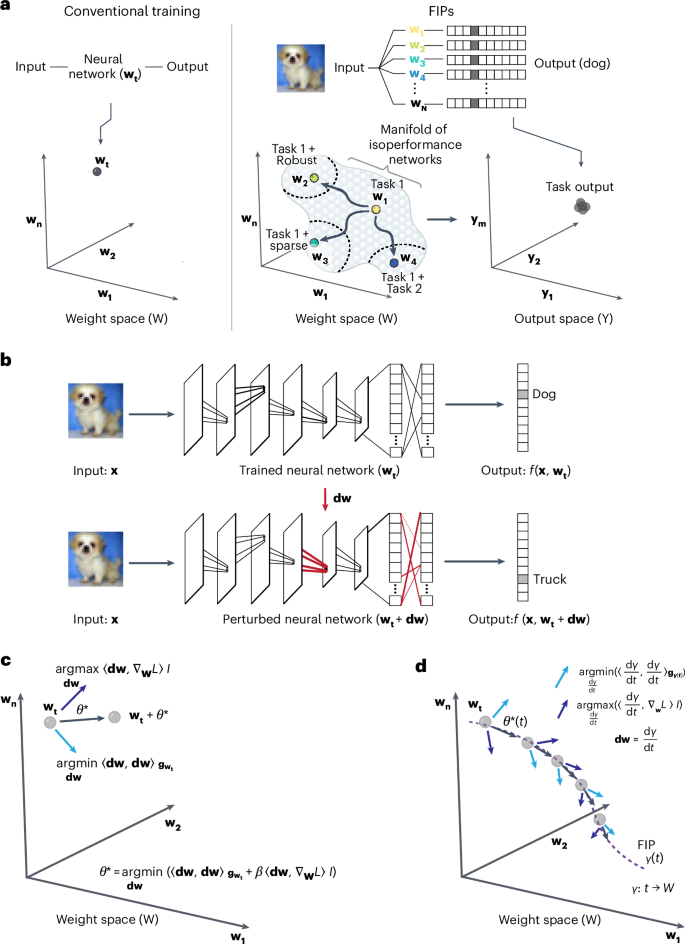
当代机器学习算法通过对特定任务的训练数据进行梯度下降,将网络权重设置为单一优化配置,从而训练人工神经网络。由此产生的网络可以在自然语言处理、图像分析和基于代理的任务中实现人类水平的性能,但缺乏人类智能所特有的灵活性和鲁棒性。在这里,我们引入了一个微分几何框架--功能不变路径,它能对训练有素的神经网络进行灵活、持续的调整,从而实现主要机器学习目标之外的次要任务,包括增加网络稀疏性和对抗鲁棒性。我们将神经网络的权重空间表述为一个弯曲的黎曼流形,该流形配备了一个度量张量,其频谱定义了权重空间中的低秩子空间,可在不丢失先验知识的情况下适应网络。我们将适应性形式化为沿着权重空间中的大地路径移动,同时搜索可满足次要目标的网络。在计算资源有限的情况下,功能不变路径算法在大型语言模型(变换器的双向编码器表示)、视觉变换器(ViT 和 DeIT)和卷积神经网络的持续学习、稀疏化和对抗鲁棒性任务中,实现了与最先进方法(包括低阶自适应)相当甚至更高的性能。本文章由计算机程序翻译,如有差异,请以英文原文为准。

Engineering flexible machine learning systems by traversing functionally invariant paths
Contemporary machine learning algorithms train artificial neural networks by setting network weights to a single optimized configuration through gradient descent on task-specific training data. The resulting networks can achieve human-level performance on natural language processing, image analysis and agent-based tasks, but lack the flexibility and robustness characteristic of human intelligence. Here we introduce a differential geometry framework—functionally invariant paths—that provides flexible and continuous adaptation of trained neural networks so that secondary tasks can be achieved beyond the main machine learning goal, including increased network sparsification and adversarial robustness. We formulate the weight space of a neural network as a curved Riemannian manifold equipped with a metric tensor whose spectrum defines low-rank subspaces in weight space that accommodate network adaptation without loss of prior knowledge. We formalize adaptation as movement along a geodesic path in weight space while searching for networks that accommodate secondary objectives. With modest computational resources, the functionally invariant path algorithm achieves performance comparable with or exceeding state-of-the-art methods including low-rank adaptation on continual learning, sparsification and adversarial robustness tasks for large language models (bidirectional encoder representations from transformers), vision transformers (ViT and DeIT) and convolutional neural networks. Machine learning often includes secondary objectives, such as sparsity or robustness. To reach these objectives efficiently, the training of a neural network has been interpreted as the exploration of functionally invariant paths in the parameter space.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Nature Machine Intelligence
Multiple-
CiteScore
36.90
自引率
2.10%
发文量
127
期刊介绍:
Nature Machine Intelligence is a distinguished publication that presents original research and reviews on various topics in machine learning, robotics, and AI. Our focus extends beyond these fields, exploring their profound impact on other scientific disciplines, as well as societal and industrial aspects. We recognize limitless possibilities wherein machine intelligence can augment human capabilities and knowledge in domains like scientific exploration, healthcare, medical diagnostics, and the creation of safe and sustainable cities, transportation, and agriculture. Simultaneously, we acknowledge the emergence of ethical, social, and legal concerns due to the rapid pace of advancements.
To foster interdisciplinary discussions on these far-reaching implications, Nature Machine Intelligence serves as a platform for dialogue facilitated through Comments, News Features, News & Views articles, and Correspondence. Our goal is to encourage a comprehensive examination of these subjects.
Similar to all Nature-branded journals, Nature Machine Intelligence operates under the guidance of a team of skilled editors. We adhere to a fair and rigorous peer-review process, ensuring high standards of copy-editing and production, swift publication, and editorial independence.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


