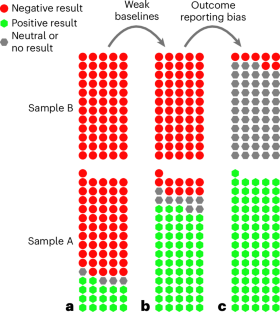
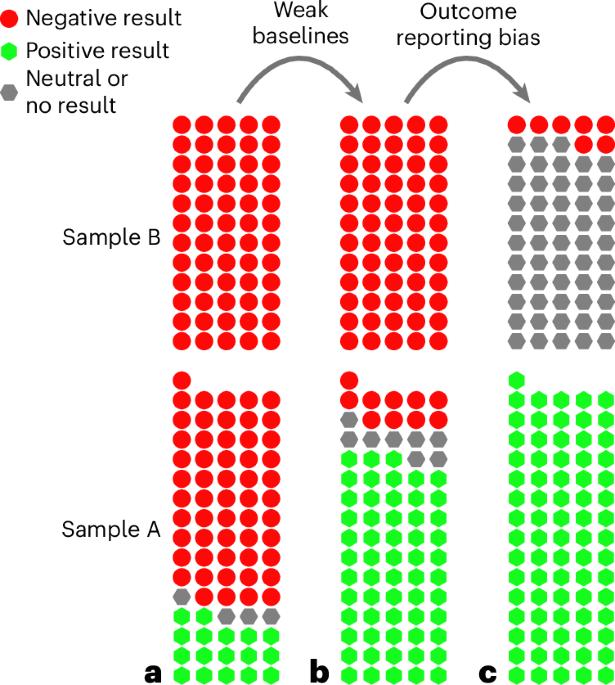
Weak baselines and reporting biases lead to overoptimism in machine learning for fluid-related partial differential equations

One of the most promising applications of machine learning in computational physics is to accelerate the solution of partial differential equations (PDEs). The key objective of machine-learning-based PDE solvers is to output a sufficiently accurate solution faster than standard numerical methods, which are used as a baseline comparison. We first perform a systematic review of the ML-for-PDE-solving literature. Out of all of the articles that report using ML to solve a fluid-related PDE and claim to outperform a standard numerical method, we determine that 79% (60/76) make a comparison with a weak baseline. Second, we find evidence that reporting biases are widespread, especially outcome reporting and publication biases. We conclude that ML-for-PDE-solving research is overoptimistic: weak baselines lead to overly positive results, while reporting biases lead to under-reporting of negative results. To a large extent, these issues seem to be caused by factors similar to those of past reproducibility crises: researcher degrees of freedom and a bias towards positive results. We call for bottom-up cultural changes to minimize biased reporting as well as top-down structural reforms to reduce perverse incentives for doing so. A systematic review of machine learning approaches to solve partial differential equations related to fluid dynamics highlights concerns about reproducibility and indicates that studies in this area have reached overly optimistic conclusions.