关于广义二项式边理想的正则猜想

IF 0.7 2区数学 Q2 MATHEMATICS

Collectanea Mathematica Pub Date : 2024-08-20 DOI:10.1007/s13348-024-00452-w

J. Anuvinda, Ranjana Mehta, Kamalesh Saha

{"title":"关于广义二项式边理想的正则猜想","authors":"J. Anuvinda, Ranjana Mehta, Kamalesh Saha","doi":"10.1007/s13348-024-00452-w","DOIUrl":null,"url":null,"abstract":"<p>In this paper, we prove the upper bound conjecture proposed by Saeedi Madani and Kiani on the Castelnuovo–Mumford regularity of generalized binomial edge ideals. We give a combinatorial upper bound of regularity for generalized binomial edge ideals, which is better than the bound claimed in that conjecture. Also, we show that the bound is tight by providing an infinite class of graphs.</p>","PeriodicalId":50993,"journal":{"name":"Collectanea Mathematica","volume":null,"pages":null},"PeriodicalIF":0.7000,"publicationDate":"2024-08-20","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On a regularity-conjecture of generalized binomial edge ideals\",\"authors\":\"J. Anuvinda, Ranjana Mehta, Kamalesh Saha\",\"doi\":\"10.1007/s13348-024-00452-w\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>In this paper, we prove the upper bound conjecture proposed by Saeedi Madani and Kiani on the Castelnuovo–Mumford regularity of generalized binomial edge ideals. We give a combinatorial upper bound of regularity for generalized binomial edge ideals, which is better than the bound claimed in that conjecture. Also, we show that the bound is tight by providing an infinite class of graphs.</p>\",\"PeriodicalId\":50993,\"journal\":{\"name\":\"Collectanea Mathematica\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.7000,\"publicationDate\":\"2024-08-20\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Collectanea Mathematica\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s13348-024-00452-w\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Collectanea Mathematica","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s13348-024-00452-w","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

在本文中，我们证明了 Saeedi Madani 和 Kiani 就广义二叉边理想的卡斯特努沃-芒福德正则性提出的上界猜想。我们给出了广义二项式边理想正则性的组合上界，它优于该猜想中的上界。此外，我们还提供了一类无限图，从而证明该约束是严密的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

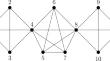
On a regularity-conjecture of generalized binomial edge ideals

查看原文本刊更多论文

On a regularity-conjecture of generalized binomial edge ideals

In this paper, we prove the upper bound conjecture proposed by Saeedi Madani and Kiani on the Castelnuovo–Mumford regularity of generalized binomial edge ideals. We give a combinatorial upper bound of regularity for generalized binomial edge ideals, which is better than the bound claimed in that conjecture. Also, we show that the bound is tight by providing an infinite class of graphs.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Collectanea Mathematica 数学-数学

CiteScore

2.70

自引率

9.10%

发文量

审稿时长

>12 weeks

期刊介绍： Collectanea Mathematica publishes original research peer reviewed papers of high quality in all fields of pure and applied mathematics. It is an international journal of the University of Barcelona and the oldest mathematical journal in Spain. It was founded in 1948 by José M. Orts. Previously self-published by the Institut de Matemàtica (IMUB) of the Universitat de Barcelona, as of 2011 it is published by Springer.