伪评估域中的准二次模组
IF 0.5
3区 数学
Q3 MATHEMATICS
引用次数: 0
摘要
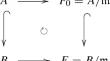
我们研究伪估值域 A 中的准二次模组,其严格单元允许有平方根。让 \(\mathfrak X_R^N\) 表示 R 模块 N 中准二次模组的集合,其中 R 是交换环。已知存在一个唯一的 A 的重环 B,使得 B 是一个具有估值群 \((G,\le )\) 的估值环,并且 B 的最大理想与 A 的最大理想重合。在上述设置中,我们找到了 \({\mathfrak {X}}_A^A\) 和 \(\prod _{g \in G,g \ge e} {\mathfrak {X}}_{F_0}^F\) 的子集之间的一一对应关系。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Quasi-quadratic modules in pseudo-valuation domain
We study quasi-quadratic modules in a pseudo-valuation domain A whose strict units admit a square root. Let \(\mathfrak X_R^N\) denote the set of quasi-quadratic modules in an R-module N, where R is a commutative ring. It is known that there exists a unique overring B of A such that B is a valuation ring with the valuation group \((G,\le )\) and the maximal ideal of B coincides with that of A. Let F be the residue field of B. In the above setting, we found a one-to-one correspondence between \({\mathfrak {X}}_A^A\) and a subset of \(\prod _{g \in G,g \ge e} {\mathfrak {X}}_{F_0}^F\).
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.40
自引率
0.00%
发文量
67
审稿时长
>12 weeks
期刊介绍:
Periodica Mathematica Hungarica is devoted to publishing research articles in all areas of pure and applied mathematics as well as theoretical computer science. To be published in the Periodica, a paper must be correct, new, and significant. Very strong submissions (upon the consent of the author) will be redirected to Acta Mathematica Hungarica.
Periodica Mathematica Hungarica is the journal of the Hungarian Mathematical Society (János Bolyai Mathematical Society). The main profile of the journal is in pure mathematics, being open to applied mathematical papers with significant mathematical content.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


