有限阿德尔上某些弗拉基米洛夫型时变哈密顿的 qp 和 pq 量化的费曼公式

IF 1.4 3区数学 Q1 MATHEMATICS

Analysis and Mathematical Physics Pub Date : 2024-08-27 DOI:10.1007/s13324-024-00965-4

Roman Urban

{"title":"有限阿德尔上某些弗拉基米洛夫型时变哈密顿的 qp 和 pq 量化的费曼公式","authors":"Roman Urban","doi":"10.1007/s13324-024-00965-4","DOIUrl":null,"url":null,"abstract":"<div>Let Q be the d-dimensional space of finite adeles over the algebraic number field K and let \\(P=Q^*\\) be its dual space. For a certain type of Vladimirov type time-dependent Hamiltonian \\(H_V(t):Q\\times P\\rightarrow {\\mathbb {C}}\\) we construct the Feynman formulas for the solution of the Cauchy problem with the Schrödinger operator <img> where the caret operator stands for the qp- or pq-quantization.</div>","PeriodicalId":48860,"journal":{"name":"Analysis and Mathematical Physics","volume":"14 5","pages":""},"PeriodicalIF":1.4000,"publicationDate":"2024-08-27","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"https://link.springer.com/content/pdf/10.1007/s13324-024-00965-4.pdf","citationCount":"0","resultStr":"{\"title\":\"Feynman formulas for qp- and pq-quantization of some Vladimirov type time-dependent Hamiltonians on finite adeles\",\"authors\":\"Roman Urban\",\"doi\":\"10.1007/s13324-024-00965-4\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<div>Let Q be the d-dimensional space of finite adeles over the algebraic number field K and let \\\\(P=Q^*\\\\) be its dual space. For a certain type of Vladimirov type time-dependent Hamiltonian \\\\(H_V(t):Q\\\\times P\\\\rightarrow {\\\\mathbb {C}}\\\\) we construct the Feynman formulas for the solution of the Cauchy problem with the Schrödinger operator <img> where the caret operator stands for the qp- or pq-quantization.</div>\",\"PeriodicalId\":48860,\"journal\":{\"name\":\"Analysis and Mathematical Physics\",\"volume\":\"14 5\",\"pages\":\"\"},\"PeriodicalIF\":1.4000,\"publicationDate\":\"2024-08-27\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"https://link.springer.com/content/pdf/10.1007/s13324-024-00965-4.pdf\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Analysis and Mathematical Physics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1007/s13324-024-00965-4\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Analysis and Mathematical Physics","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1007/s13324-024-00965-4","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

让 Q 是代数数域 K 上的 d 维有限阿德尔空间，让 \(P=Q^*\)是它的对偶空间。对于某类弗拉基米洛夫型时变哈密顿（H_V(t):Q\times P\rightarrow {\mathbb {C}}\），我们用薛定谔算子构造了考希问题解的费曼公式，其中caret算子代表qp-或pq-量子化。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

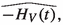
Feynman formulas for qp- and pq-quantization of some Vladimirov type time-dependent Hamiltonians on finite adeles

查看原文本刊更多论文

Feynman formulas for qp- and pq-quantization of some Vladimirov type time-dependent Hamiltonians on finite adeles

Let Q be the d-dimensional space of finite adeles over the algebraic number field K and let \(P=Q^*\) be its dual space. For a certain type of Vladimirov type time-dependent Hamiltonian \(H_V(t):Q\times P\rightarrow {\mathbb {C}}\) we construct the Feynman formulas for the solution of the Cauchy problem with the Schrödinger operator where the caret operator stands for the qp- or pq-quantization.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Analysis and Mathematical Physics MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

2.70

自引率

0.00%

发文量

122

期刊介绍： Analysis and Mathematical Physics (AMP) publishes current research results as well as selected high-quality survey articles in real, complex, harmonic; and geometric analysis originating and or having applications in mathematical physics. The journal promotes dialog among specialists in these areas.