部分充满粘性流体的物体系统在弹性阻尼力作用下的正常振荡问题

IF 0.8 Q2 MATHEMATICS

Lobachevskii Journal of Mathematics Pub Date : 2024-08-22 DOI:10.1134/s1995080224601176

K. V. Forduk, D. A. Zakora

{"title":"部分充满粘性流体的物体系统在弹性阻尼力作用下的正常振荡问题","authors":"K. V. Forduk, D. A. Zakora","doi":"10.1134/s1995080224601176","DOIUrl":null,"url":null,"abstract":"<h3 data-test=\"abstract-sub-heading\">Abstract</h3><p>In this paper, we study the problem on normal oscillations of a system of bodies partially filled with viscous fluids under the action of elastic and damping forces. It is proven that the nonzero spectrum of the problem is discrete and condenses towards zero and infinity. Asymptotic formulae for the eigenvalues are proved. A theorem on the <span>\\(p\\)</span>-basicity of the system of root elements of the problem is proven.</p>","PeriodicalId":46135,"journal":{"name":"Lobachevskii Journal of Mathematics","volume":"59 1","pages":""},"PeriodicalIF":0.8000,"publicationDate":"2024-08-22","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"The Problem on Normal Oscillations of a System of Bodies Partially Filled with Viscous Fluids under the Action of Elastic-Damping Forces\",\"authors\":\"K. V. Forduk, D. A. Zakora\",\"doi\":\"10.1134/s1995080224601176\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<h3 data-test=\\\"abstract-sub-heading\\\">Abstract</h3><p>In this paper, we study the problem on normal oscillations of a system of bodies partially filled with viscous fluids under the action of elastic and damping forces. It is proven that the nonzero spectrum of the problem is discrete and condenses towards zero and infinity. Asymptotic formulae for the eigenvalues are proved. A theorem on the <span>\\\\(p\\\\)</span>-basicity of the system of root elements of the problem is proven.</p>\",\"PeriodicalId\":46135,\"journal\":{\"name\":\"Lobachevskii Journal of Mathematics\",\"volume\":\"59 1\",\"pages\":\"\"},\"PeriodicalIF\":0.8000,\"publicationDate\":\"2024-08-22\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Lobachevskii Journal of Mathematics\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1134/s1995080224601176\",\"RegionNum\":0,\"RegionCategory\":null,\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Lobachevskii Journal of Mathematics","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1134/s1995080224601176","RegionNum":0,"RegionCategory":null,"ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

摘要本文研究了在弹性力和阻尼力作用下，部分充满粘性流体的物体系统的法向振荡问题。研究证明，该问题的非零谱是离散的，并向零和无穷大方向凝聚。证明了特征值的渐近公式。证明了问题根元素系统的基本性定理。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

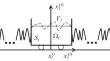
The Problem on Normal Oscillations of a System of Bodies Partially Filled with Viscous Fluids under the Action of Elastic-Damping Forces

查看原文本刊更多论文

The Problem on Normal Oscillations of a System of Bodies Partially Filled with Viscous Fluids under the Action of Elastic-Damping Forces

Abstract

In this paper, we study the problem on normal oscillations of a system of bodies partially filled with viscous fluids under the action of elastic and damping forces. It is proven that the nonzero spectrum of the problem is discrete and condenses towards zero and infinity. Asymptotic formulae for the eigenvalues are proved. A theorem on the \(p\)-basicity of the system of root elements of the problem is proven.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Lobachevskii Journal of Mathematics MATHEMATICS-

CiteScore

1.50

自引率

42.90%

发文量

127

期刊介绍： Lobachevskii Journal of Mathematics is an international peer reviewed journal published in collaboration with the Russian Academy of Sciences and Kazan Federal University. The journal covers mathematical topics associated with the name of famous Russian mathematician Nikolai Lobachevsky (Lobachevskii). The journal publishes research articles on geometry and topology, algebra, complex analysis, functional analysis, differential equations and mathematical physics, probability theory and stochastic processes, computational mathematics, mathematical modeling, numerical methods and program complexes, computer science, optimal control, and theory of algorithms as well as applied mathematics. The journal welcomes manuscripts from all countries in the English language.