附着涡速度梯度矩的缩放规律
IF 2.5
3区 物理与天体物理
Q2 PHYSICS, FLUIDS & PLASMAS
引用次数: 0
摘要
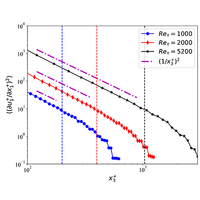
汤森附着涡模型(AEM)是解释和预测壁面湍流对数区最广泛使用的模型之一。汤森率先提出了附壁涡呈现自相似速度分布的假设。这一假设推导出了对数区域的速度方差标度。特别是,附壁涡在中等尺度下被提取出来,并被证明在对数区域包含了最多的动能。在本文中,我们利用 AEM 分析得出了附着涡速度梯度矩的标度。中等尺度附着涡提取的直接数值模拟数据与推导出的标度有很好的一致性。此外,比较了不同尺度结构对速度梯度矩的贡献,结果表明所有尺度速度梯度的壁面标度是中等尺度附着涡的一半。这也表明小尺度涡对对数区域速度梯度的影响不可忽略。此外,速度赫塞斯矩也存在偏差,这对今后改进附着涡的提取方法有所启发。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Scaling laws of velocity gradient moments of attached eddies
Townsend's attached-eddy model (AEM) is one of the most widely used models in explaining and predicting the logarithmic region of wall turbulence. Townsend pioneered the postulate that wall-attached eddies exhibit self-similar velocity distributions. This premise has led to the derivation of velocity variance scalings in the logarithmic region. In particular, the attached eddies have been extracted at moderate scales and have been illustrated to contain the most kinetic energies in the logarithmic region. In the present contribution, we derive analytically the scalings of the moments of velocity gradients of attached eddies by using the AEM. The direct numerical simulation data with the moderate-scale extraction of attached eddies show good agreement with the derived scalings. Moreover, the contributions of different-scale structures to the moments of velocity gradients are compared, showing that the wall scalings of all-scale velocity gradients are interestingly half of moderate-scale attached eddies. This also indicates the non-negligible influence of the small-scale eddies on the velocity gradients in the logarithmic region. In addition, there are departures in the moments of velocity Hessian, inspiring future improvement in the extraction method of attached eddies.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
Physical Review Fluids
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
5.10
自引率
11.10%
发文量
488
期刊介绍:
Physical Review Fluids is APS’s newest online-only journal dedicated to publishing innovative research that will significantly advance the fundamental understanding of fluid dynamics. Physical Review Fluids expands the scope of the APS journals to include additional areas of fluid dynamics research, complements the existing Physical Review collection, and maintains the same quality and reputation that authors and subscribers expect from APS. The journal is published with the endorsement of the APS Division of Fluid Dynamics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


