自由分解空间

IF 0.7 2区数学 Q2 MATHEMATICS

Collectanea Mathematica Pub Date : 2024-09-02 DOI:10.1007/s13348-024-00446-8

Philip Hackney, Joachim Kock

{"title":"自由分解空间","authors":"Philip Hackney, Joachim Kock","doi":"10.1007/s13348-024-00446-8","DOIUrl":null,"url":null,"abstract":"We introduce the notion of free decomposition spaces: they are simplicial spaces freely generated by inert maps. We show that left Kan extension along the inclusion takes general objects to Möbius decomposition spaces and general maps to CULF maps. We establish an equivalence of \\(\\infty \\)-categories <img alt=\"\" src=\"//media.springernature.com/lw177/springer-static/image/art%3A10.1007%2Fs13348-024-00446-8/MediaObjects/13348_2024_446_IEq3_HTML.gif\" style=\"width:177px;max-width:none;\"/>. Although free decomposition spaces are rather simple objects, they abound in combinatorics: it seems that all comultiplications of deconcatenation type arise from free decomposition spaces. We give an extensive list of examples, including quasi-symmetric functions.","PeriodicalId":50993,"journal":{"name":"Collectanea Mathematica","volume":null,"pages":null},"PeriodicalIF":0.7000,"publicationDate":"2024-09-02","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Free decomposition spaces\",\"authors\":\"Philip Hackney, Joachim Kock\",\"doi\":\"10.1007/s13348-024-00446-8\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"We introduce the notion of free decomposition spaces: they are simplicial spaces freely generated by inert maps. We show that left Kan extension along the inclusion takes general objects to Möbius decomposition spaces and general maps to CULF maps. We establish an equivalence of \\\\(\\\\infty \\\\)-categories <img alt=\\\"\\\" src=\\\"//media.springernature.com/lw177/springer-static/image/art%3A10.1007%2Fs13348-024-00446-8/MediaObjects/13348_2024_446_IEq3_HTML.gif\\\" style=\\\"width:177px;max-width:none;\\\"/>. Although free decomposition spaces are rather simple objects, they abound in combinatorics: it seems that all comultiplications of deconcatenation type arise from free decomposition spaces. We give an extensive list of examples, including quasi-symmetric functions.\",\"PeriodicalId\":50993,\"journal\":{\"name\":\"Collectanea Mathematica\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.7000,\"publicationDate\":\"2024-09-02\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Collectanea Mathematica\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s13348-024-00446-8\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Collectanea Mathematica","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s13348-024-00446-8","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们引入了自由分解空间的概念：它们是由惰性映射自由生成的单纯空间。我们证明了沿着包含的左坎扩展可以把一般对象带到莫比乌斯分解空间，把一般映射带到 CULF 映射。我们建立了一个等价的（infty）范畴。虽然自由分解空间是相当简单的对象，但它们在组合学中却比比皆是：似乎所有去分解类型的相乘都产生于自由分解空间。我们列举了大量例子，包括准对称函数。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

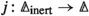
Free decomposition spaces

查看原文本刊更多论文

Free decomposition spaces

We introduce the notion of free decomposition spaces: they are simplicial spaces freely generated by inert maps. We show that left Kan extension along the inclusion takes general objects to Möbius decomposition spaces and general maps to CULF maps. We establish an equivalence of \(\infty \)-categories . Although free decomposition spaces are rather simple objects, they abound in combinatorics: it seems that all comultiplications of deconcatenation type arise from free decomposition spaces. We give an extensive list of examples, including quasi-symmetric functions.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Collectanea Mathematica 数学-数学

CiteScore

2.70

自引率

9.10%

发文量

审稿时长

>12 weeks

期刊介绍： Collectanea Mathematica publishes original research peer reviewed papers of high quality in all fields of pure and applied mathematics. It is an international journal of the University of Barcelona and the oldest mathematical journal in Spain. It was founded in 1948 by José M. Orts. Previously self-published by the Institut de Matemàtica (IMUB) of the Universitat de Barcelona, as of 2011 it is published by Springer.