On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture

We investigate the Gross–Prasad conjecture and its refinement for the Bessel periods in the case of 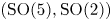$(\mathrm {SO}(5), \mathrm {SO}(2))$. In particular, by combining several theta correspondences, we prove the Ichino–Ikeda-type formula for any tempered irreducible cuspidal automorphic representation. As a corollary of our formula, we prove an explicit formula relating certain weighted averages of Fourier coefficients of holomorphic Siegel cusp forms of degree two, which are Hecke eigenforms, to central special values of 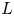$L$-functions. The formula is regarded as a natural generalization of the Böcherer conjecture to the non-trivial toroidal character case.