对流双相问题的正解

IF 1.1 3区数学 Q1 MATHEMATICS

Results in Mathematics Pub Date : 2024-08-26 DOI:10.1007/s00025-024-02262-9

Nikolao S. Papageorgiou, Zijia Peng

{"title":"对流双相问题的正解","authors":"Nikolao S. Papageorgiou, Zijia Peng","doi":"10.1007/s00025-024-02262-9","DOIUrl":null,"url":null,"abstract":"<p>We consider a nonlinear Dirichlet problem driven by the double phase differential operator and a reaction that has the competing effects of a parametric concave term and of a convective perturbation. Using truncation and comparison techniques and the theory of nonlinear operators of monotone type, we show that for all small values of the parameter, the problem has a bounded positive solution.</p>","PeriodicalId":54490,"journal":{"name":"Results in Mathematics","volume":"22 1","pages":""},"PeriodicalIF":1.1000,"publicationDate":"2024-08-26","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Positive Solutions for Convective Double Phase Problems\",\"authors\":\"Nikolao S. Papageorgiou, Zijia Peng\",\"doi\":\"10.1007/s00025-024-02262-9\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We consider a nonlinear Dirichlet problem driven by the double phase differential operator and a reaction that has the competing effects of a parametric concave term and of a convective perturbation. Using truncation and comparison techniques and the theory of nonlinear operators of monotone type, we show that for all small values of the parameter, the problem has a bounded positive solution.</p>\",\"PeriodicalId\":54490,\"journal\":{\"name\":\"Results in Mathematics\",\"volume\":\"22 1\",\"pages\":\"\"},\"PeriodicalIF\":1.1000,\"publicationDate\":\"2024-08-26\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Results in Mathematics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00025-024-02262-9\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Results in Mathematics","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00025-024-02262-9","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们考虑了一个由双相微分算子和反应驱动的非线性迪里夏特问题，该反应具有参数凹项和对流扰动的竞争效应。利用截断和比较技术以及单调型非线性算子理论，我们证明了对于所有小的参数值，该问题都有一个有界的正解。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

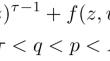
Positive Solutions for Convective Double Phase Problems

查看原文本刊更多论文

Positive Solutions for Convective Double Phase Problems

We consider a nonlinear Dirichlet problem driven by the double phase differential operator and a reaction that has the competing effects of a parametric concave term and of a convective perturbation. Using truncation and comparison techniques and the theory of nonlinear operators of monotone type, we show that for all small values of the parameter, the problem has a bounded positive solution.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Results in Mathematics 数学-数学

CiteScore

1.90

自引率

4.50%

发文量

198

审稿时长

6-12 weeks

期刊介绍： Results in Mathematics (RM) publishes mainly research papers in all fields of pure and applied mathematics. In addition, it publishes summaries of any mathematical field and surveys of any mathematical subject provided they are designed to advance some recent mathematical development.