半总支配数为其阶数一半的图

IF 0.6 4区数学 Q3 MATHEMATICS

Bulletin of the Australian Mathematical Society Pub Date : 2024-09-13 DOI:10.1017/s0004972724000509

JIE CHEN, SHOU-JUN XU

{"title":"半总支配数为其阶数一半的图","authors":"JIE CHEN, SHOU-JUN XU","doi":"10.1017/s0004972724000509","DOIUrl":null,"url":null,"abstract":"In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by <img data-mimesubtype=\"png\" data-type=\"\" src=\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20240912125800045-0875:S0004972724000509:S0004972724000509_inline1.png\">$\\gamma _{t2}(G)$</img>, is the minimum cardinality of a semitotal dominating set in G. Goddard, Henning and McPillan [‘Semitotal domination in graphs’, Utilitas Math. 94 (2014), 67–81] characterised the trees and graphs of minimum degree 2 with semitotal domination number half their order. In this paper, we characterise all graphs whose semitotal domination number is half their order.","PeriodicalId":50720,"journal":{"name":"Bulletin of the Australian Mathematical Society","volume":null,"pages":null},"PeriodicalIF":0.6000,"publicationDate":"2024-09-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER\",\"authors\":\"JIE CHEN, SHOU-JUN XU\",\"doi\":\"10.1017/s0004972724000509\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by <img data-mimesubtype=\\\"png\\\" data-type=\\\"\\\" src=\\\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20240912125800045-0875:S0004972724000509:S0004972724000509_inline1.png\\\">$\\\\gamma _{t2}(G)$</img>, is the minimum cardinality of a semitotal dominating set in G. Goddard, Henning and McPillan [‘Semitotal domination in graphs’, Utilitas Math. 94 (2014), 67–81] characterised the trees and graphs of minimum degree 2 with semitotal domination number half their order. In this paper, we characterise all graphs whose semitotal domination number is half their order.\",\"PeriodicalId\":50720,\"journal\":{\"name\":\"Bulletin of the Australian Mathematical Society\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-09-13\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Bulletin of the Australian Mathematical Society\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1017/s0004972724000509\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Bulletin of the Australian Mathematical Society","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1017/s0004972724000509","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

在无孤立图 G 中，如果顶点子集 S 是 G 的支配集，且 S 中的每个顶点与 S 中另一个顶点的距离都在 2 以内，则该顶点子集 S 是 G 的半总支配集。G 的半总支配数用 $\gamma _{t2}(G)$ 表示，是 G 中半总支配集的最小心性。Goddard、Henning 和 McPillan ['图中的半总支配数'，Utilitas Math.在本文中，我们将描述所有半总支配数为其阶数一半的图的特征。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

查看原文本刊更多论文

GRAPHS WITH SEMITOTAL DOMINATION NUMBER HALF THEIR ORDER

In an isolate-free graph G, a subset S of vertices is a semitotal dominating set of G if it is a dominating set of G and every vertex in S is within distance 2 of another vertex of S. The semitotal domination number of G, denoted by 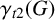$\gamma _{t2}(G)$, is the minimum cardinality of a semitotal dominating set in G. Goddard, Henning and McPillan [‘Semitotal domination in graphs’, Utilitas Math. 94 (2014), 67–81] characterised the trees and graphs of minimum degree 2 with semitotal domination number half their order. In this paper, we characterise all graphs whose semitotal domination number is half their order.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Bulletin of the Australian Mathematical Society 数学-数学

CiteScore

1.20

自引率

14.30%

发文量

149

审稿时长

4-8 weeks

期刊介绍： Bulletin of the Australian Mathematical Society aims at quick publication of original research in all branches of mathematics. Papers are accepted only after peer review but editorial decisions on acceptance or otherwise are taken quickly, normally within a month of receipt of the paper. The Bulletin concentrates on presenting new and interesting results in a clear and attractive way. Published Bi-monthly Published for the Australian Mathematical Society