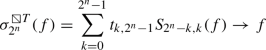
Approximation by Subsequences of Matrix Transform Means of Some Two-Dimensional Rectangle Walsh–Fourier Series

In the present paper we discuss the rate of the approximation by the matrix transform of special partial sums of some two-dimensional rectangle (decreasing diagonal) Walsh-Fourier series in \(L^p(G^{2})\) space (\(1\le p <\infty \)) and in \(C(G^{2})\). It implies in some special case

norm convergence. We also show an application of our results for Lipschitz functions. At the end of the paper we show the most important result, the almost everywhere convergence theorem. We note that T summation is a common generalization of the following known summation methods Cesàro, Weierstrass, Riesz and Picar and Bessel methods.