选定二叉树态中的纠缠:迪克态或总自旋态或粒子数投影 BCS 态
IF 3.4
2区 物理与天体物理
Q1 Physics and Astronomy
引用次数: 0
摘要
二叉树态(BTS)是指在一组量子比特构成的量子寄存器基础上可以依次分解的态。当全局对称性(如总自旋对称性或粒子数对称性)被强加时,这种状态有时会自然出现在用福克空间处理的多体系统中。例如迪克态,即具有单个自旋1/2的一组粒子的总自旋特征态,或者通过将BCS态投影到粒子数而得到的态,在小型超流体系统中也称为投影BCS态。从描述 n 个量子比特或轨道集的 BTS 开始,分析 k 个量子比特的任何子集的纠缠熵。具体地说,我们开发了一种实用方法来获取相关子系统的 k 量子位或 k 粒子冯-诺依曼纠缠熵。讨论了这些熵的特性,包括缩放特性、上限或这些熵如何与波动相关。文中给出了迪克态和投影 BCS 态的示例。本文章由计算机程序翻译,如有差异,请以英文原文为准。
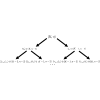
Entanglement in selected binary tree states: Dicke or total spin states or particle-number-projected BCS states
Binary tree states (BTSs) are states whose decomposition on a quantum register basis formed by a set of qubits can be made sequentially. Such states sometimes appear naturally in many-body systems treated in Fock space when a global symmetry is imposed, such as the total spin or particle number symmetries. Examples are the Dicke states, the eigenstates of the total spin for a set of particles having individual spin , or states obtained by projecting a BCS states onto particle number, also called projected BCS in small superfluid systems. Starting from a BTS described on the set of qubits or orbitals, the entanglement entropy of any subset of qubits is analyzed. Specifically, a practical method is developed to access the -qubit or -particle von Neumann entanglement entropy of the subsystem of interest. Properties of these entropies are discussed, including scaling properties, upper bounds, or how these entropies correlate with fluctuations. Illustrations are given for the Dicke state and the projected BCS states.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Physical Review C
物理-物理:核物理
CiteScore
5.70
自引率
35.50%
发文量
0
审稿时长
1-2 weeks
期刊介绍:
Physical Review C (PRC) is a leading journal in theoretical and experimental nuclear physics, publishing more than two-thirds of the research literature in the field.
PRC covers experimental and theoretical results in all aspects of nuclear physics, including:
Nucleon-nucleon interaction, few-body systems
Nuclear structure
Nuclear reactions
Relativistic nuclear collisions
Hadronic physics and QCD
Electroweak interaction, symmetries
Nuclear astrophysics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


