论幂律流体边界层楔形流问题的正自相似解
IF 1.4
4区 工程技术
Q2 ENGINEERING, MULTIDISCIPLINARY
引用次数: 0
摘要
我们首先研究了外部流加速时不可压缩粘性幂律流体二维边界层方程正自相似解的存在性和唯一性,然后推导了壁面剪应力率的边界。对于剪切增厚流体,我们证明与外部流的匹配发生在有限距离内。此外,我们还研究了剪切稀化流体正解在无穷远处的渐近行为。本文章由计算机程序翻译,如有差异,请以英文原文为准。
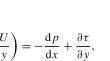
On the positive self-similar solutions of the boundary-layer wedge flow problem of a power-law fluid
We first study the existence and uniqueness of a positive self-similar solution of the 2D boundary-layer equations of an incompressible viscous power-law fluid when the external flow is accelerating, and then we derive the bounds of the wall shear stress rate. For shear-thickening fluids, we show that the matching with the external flow occurs at a finite distance. Furthermore, we also investigate the asymptotic behaviour at infinity of positive solutions in the case of shear-thinning fluids.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Journal of Engineering Mathematics
工程技术-工程:综合
CiteScore
2.10
自引率
7.70%
发文量
44
审稿时长
6 months
期刊介绍:
The aim of this journal is to promote the application of mathematics to problems from engineering and the applied sciences. It also aims to emphasize the intrinsic unity, through mathematics, of the fundamental problems of applied and engineering science. The scope of the journal includes the following:
• Mathematics: Ordinary and partial differential equations, Integral equations, Asymptotics, Variational and functional−analytic methods, Numerical analysis, Computational methods.
• Applied Fields: Continuum mechanics, Stability theory, Wave propagation, Diffusion, Heat and mass transfer, Free−boundary problems; Fluid mechanics: Aero− and hydrodynamics, Boundary layers, Shock waves, Fluid machinery, Fluid−structure interactions, Convection, Combustion, Acoustics, Multi−phase flows, Transition and turbulence, Creeping flow, Rheology, Porous−media flows, Ocean engineering, Atmospheric engineering, Non-Newtonian flows, Ship hydrodynamics; Solid mechanics: Elasticity, Classical mechanics, Nonlinear mechanics, Vibrations, Plates and shells, Fracture mechanics; Biomedical engineering, Geophysical engineering, Reaction−diffusion problems; and related areas.
The Journal also publishes occasional invited ''Perspectives'' articles by distinguished researchers reviewing and bringing their authoritative overview to recent developments in topics of current interest in their area of expertise. Authors wishing to suggest topics for such articles should contact the Editors-in-Chief directly.
Prospective authors are encouraged to consult recent issues of the journal in order to judge whether or not their manuscript is consistent with the style and content of published papers.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


