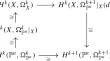
Vanishing theorem for Hodge ideals on smooth hypersurfaces

We use a Koszul-type resolution to prove a weak version of Bott’s vanishing theorem for smooth hypersurfaces in \(\mathbb {P}^n\) and use this result to prove a vanishing theorem for Hodge ideals associated to an effective Cartier divisor on a hypersurface. This extends an earlier result of Mustaţă and Popa.