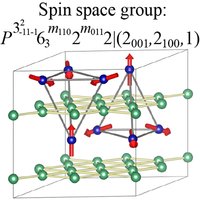
Enumeration and Representation Theory of Spin Space Groups

Fundamental physical properties, such as phase transitions, electronic structures, and spin excitations, in all magnetic ordered materials, were ultimately believed to rely on the symmetry theory of magnetic space groups. Recently, it has come to light that a more comprehensive group, known as the spin space group (SSG), which combines separate spin and spatial operations, is necessary to fully characterize the geometry and underlying properties of magnetic ordered materials. However, the basic theory of SSG has seldom been developed. In this work, we present a systematic study of the enumeration and the representation theory of the SSG. Starting from the 230 crystallographic space groups and finite translation groups with a maximum order of eight, we establish an extensive collection of over 100 000 SSGs under a four-index nomenclature as well as international notation. We then identify inequivalent SSGs specifically applicable to collinear, coplanar, and noncoplanar magnetic configurations. To facilitate the identification of the SSG, we develop an online program that can determine the SSG symmetries of any magnetic ordered crystal. Moreover, we derive the irreducible corepresentations of the little group in momentum space within the SSG framework. Finally, we illustrate the SSG symmetries and physical effects beyond the framework of magnetic space groups through several representative material examples, including a candidate altermagnet ${\mathrm{RuO}}_2$, spiral spin polarization in the coplanar antiferromagnet ${\mathrm{CeAuAl}}_3$, and geometric Hall effect in the noncoplanar antiferromagnet ${\mathrm{CoNb}}_3{\mathrm{S}}_6$. Our work advances the field of group theory in describing magnetic ordered materials, opening up avenues for deeper comprehension and further exploration of emergent phenomena in magnetic materials.