具有非局部条件和弱值非线性的反常扩散方程中的参数识别

IF 2.5 2区数学 Q1 MATHEMATICS

Fractional Calculus and Applied Analysis Pub Date : 2024-08-26 DOI:10.1007/s13540-024-00329-6

Nguyen Thi Van Anh, Bui Thi Hai Yen

{"title":"具有非局部条件和弱值非线性的反常扩散方程中的参数识别","authors":"Nguyen Thi Van Anh, Bui Thi Hai Yen","doi":"10.1007/s13540-024-00329-6","DOIUrl":null,"url":null,"abstract":"<p>The paper deals with a source identification problem of the anomalous diffusion equations from nonlocal final data observations where the nonlinearity probably takes values in Hilbert scales. The existence and uniqueness results are proved by establishing some estimates for resolvent operators and using the embedding theorems. We also study regularity results for this equation in terms of the Hölder continuity of mild solutions. Finally, the multi-term fractional diffusion equations with polynomial nonlinearities and the ultra-slow diffusions are considered as illustrative applications.</p>","PeriodicalId":48928,"journal":{"name":"Fractional Calculus and Applied Analysis","volume":"12 1","pages":""},"PeriodicalIF":2.5000,"publicationDate":"2024-08-26","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Parameter identification in anomalous diffusion equations with nonlocal conditions and weak-valued nonlinearities\",\"authors\":\"Nguyen Thi Van Anh, Bui Thi Hai Yen\",\"doi\":\"10.1007/s13540-024-00329-6\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>The paper deals with a source identification problem of the anomalous diffusion equations from nonlocal final data observations where the nonlinearity probably takes values in Hilbert scales. The existence and uniqueness results are proved by establishing some estimates for resolvent operators and using the embedding theorems. We also study regularity results for this equation in terms of the Hölder continuity of mild solutions. Finally, the multi-term fractional diffusion equations with polynomial nonlinearities and the ultra-slow diffusions are considered as illustrative applications.</p>\",\"PeriodicalId\":48928,\"journal\":{\"name\":\"Fractional Calculus and Applied Analysis\",\"volume\":\"12 1\",\"pages\":\"\"},\"PeriodicalIF\":2.5000,\"publicationDate\":\"2024-08-26\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Fractional Calculus and Applied Analysis\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s13540-024-00329-6\",\"RegionNum\":2,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q1\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Fractional Calculus and Applied Analysis","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s13540-024-00329-6","RegionNum":2,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q1","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

本文讨论了非局部最终数据观测的异常扩散方程的源识别问题，其中非线性可能在希尔伯特尺度上取值。通过建立对 resolvent 算子的一些估计并使用嵌入定理，证明了存在性和唯一性结果。我们还从温和解的赫尔德连续性角度研究了该方程的正则性结果。最后，我们还考虑了具有多项式非线性的多期分数扩散方程和超慢扩散作为说明性应用。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

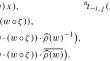
Parameter identification in anomalous diffusion equations with nonlocal conditions and weak-valued nonlinearities

查看原文本刊更多论文

Parameter identification in anomalous diffusion equations with nonlocal conditions and weak-valued nonlinearities

The paper deals with a source identification problem of the anomalous diffusion equations from nonlocal final data observations where the nonlinearity probably takes values in Hilbert scales. The existence and uniqueness results are proved by establishing some estimates for resolvent operators and using the embedding theorems. We also study regularity results for this equation in terms of the Hölder continuity of mild solutions. Finally, the multi-term fractional diffusion equations with polynomial nonlinearities and the ultra-slow diffusions are considered as illustrative applications.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Fractional Calculus and Applied Analysis MATHEMATICS, APPLIED-MATHEMATICS, INTERDISCIPLINARY APPLICATIONS

CiteScore

4.70

自引率

16.70%

发文量

101

期刊介绍： Fractional Calculus and Applied Analysis (FCAA, abbreviated in the World databases as Fract. Calc. Appl. Anal. or FRACT CALC APPL ANAL) is a specialized international journal for theory and applications of an important branch of Mathematical Analysis (Calculus) where differentiations and integrations can be of arbitrary non-integer order. The high standards of its contents are guaranteed by the prominent members of Editorial Board and the expertise of invited external reviewers, and proven by the recently achieved high values of impact factor (JIF) and impact rang (SJR), launching the journal to top places of the ranking lists of Thomson Reuters and Scopus.