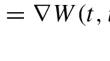
Multiplicity of solutions for fractional Hamiltonian systems with combined nonlinearities and without coercive conditions

Consider the following fractional Hamiltonian system:

$$\begin{aligned} \left\{ \begin{array}{l} _{t}D_{\infty }^{\alpha }(_{-\infty }D_{t}^{\alpha }u)(t)+L(t)u(t)=\nabla W(t,u(t)),\ t\in \mathbb {R}\\ u\in H^{\alpha }(\mathbb {R}). \end{array}\right. \end{aligned}$$

Here, \(_{t}D_{\infty }^{\alpha }\) and \(_{-\infty }D_{t}^{\alpha }\) represent the Liouville-Weyl fractional derivatives of order \(\frac{1}{2}< \alpha < 1\), \(L \in C(\mathbb {R}, \mathbb {R}^{N^2})\) is a symmetric matrix, and \(W \in C^{1}(\mathbb {R} \times \mathbb {R}^N, \mathbb {R})\). By applying the Fountain Theorem and the Dual Fountain Theorem, we demonstrate that this system admits two distinct sequences of solutions under the condition that L meets a new non-coercive criterion, and the potential W(t, x) exhibits combined nonlinearities.