有限高度山脊上的附着和分离旋转流
IF 2.5
3区 物理与天体物理
Q2 PHYSICS, FLUIDS & PLASMAS
引用次数: 0
摘要
本文使用基于稳定有限元的数值方法讨论了旋转对山脊上高雷诺数流动边界层的影响,该方法可捕捉高达 106 阶雷诺数的稳定解。其结果与浅层流的边界层计算结果进行了验证,并与 Machicoane 等人[Phys. Rev. Fluids 3, 034801 (2018)]报告的深层流实验观测结果进行了验证。在考虑的所有情况下,只要流动的罗斯比数小于某个临界罗斯比数,边界层即使在任意大的雷诺数下也会保持附着。在任何固定的罗斯比数大于该临界值的情况下,气流都会在足够高的雷诺数下脱离,从而在脊的边缘形成一个稳定的再循环区域。在更高的雷诺数下,也找不到稳定流。这种稳定解的消失密切再现了在实验室中看到的向不稳定性的过渡。本文章由计算机程序翻译,如有差异,请以英文原文为准。
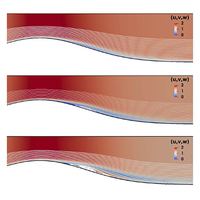
Attached and separated rotating flow over a finite height ridge
This article discusses the effect of rotation on the boundary layer in high Reynolds number flow over a ridge using a numerical method based on stabilized finite elements that captures steady solutions up to a Reynolds number of order . The results are validated against boundary layer computations in shallow flows and for deep flows against experimental observations reported in Machicoane et al. [Phys. Rev. Fluids 3, 034801 (2018)]. In all cases considered the boundary layer remains attached, even at arbitrarily large Reynolds numbers, provided the Rossby number of the flow is less than some critical Rossby number of order unity. At any fixed Rossby number larger than this critical value, the flow detaches at sufficiently high Reynolds number to form a steady recirculating region in the lee of the ridge. At even higher Reynolds numbers no steady flow is found. This disappearance of steady solutions closely reproduces the transition to unsteadiness seen in the laboratory.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
Physical Review Fluids
Chemical Engineering-Fluid Flow and Transfer Processes
CiteScore
5.10
自引率
11.10%
发文量
488
期刊介绍:
Physical Review Fluids is APS’s newest online-only journal dedicated to publishing innovative research that will significantly advance the fundamental understanding of fluid dynamics. Physical Review Fluids expands the scope of the APS journals to include additional areas of fluid dynamics research, complements the existing Physical Review collection, and maintains the same quality and reputation that authors and subscribers expect from APS. The journal is published with the endorsement of the APS Division of Fluid Dynamics.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


