封闭流形上具有负幂和符号变化非线性的哈代-索博列夫方程

IF 0.9 3区数学 Q2 MATHEMATICS

Journal of Pseudo-Differential Operators and Applications Pub Date : 2024-07-30 DOI:10.1007/s11868-024-00630-1

Nanbo Chen, Honghong Liang, Zhihua Huang, Xiaochun Liu

{"title":"封闭流形上具有负幂和符号变化非线性的哈代-索博列夫方程","authors":"Nanbo Chen, Honghong Liang, Zhihua Huang, Xiaochun Liu","doi":"10.1007/s11868-024-00630-1","DOIUrl":null,"url":null,"abstract":"<p>We study a class of Hardy-Sobolev equations containing both sign-changing and negative power terms on closed Riemannian manifolds. With the help of a modified Nehari manifold method and some variational techniques, the existence and multiplicity of positive weak solutions are established, along with blow-up behavior analysis.</p>","PeriodicalId":48793,"journal":{"name":"Journal of Pseudo-Differential Operators and Applications","volume":"41 1","pages":""},"PeriodicalIF":0.9000,"publicationDate":"2024-07-30","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Hardy–Sobolev equation with negative power and sign-changing nonlinearity on closed manifolds\",\"authors\":\"Nanbo Chen, Honghong Liang, Zhihua Huang, Xiaochun Liu\",\"doi\":\"10.1007/s11868-024-00630-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>We study a class of Hardy-Sobolev equations containing both sign-changing and negative power terms on closed Riemannian manifolds. With the help of a modified Nehari manifold method and some variational techniques, the existence and multiplicity of positive weak solutions are established, along with blow-up behavior analysis.</p>\",\"PeriodicalId\":48793,\"journal\":{\"name\":\"Journal of Pseudo-Differential Operators and Applications\",\"volume\":\"41 1\",\"pages\":\"\"},\"PeriodicalIF\":0.9000,\"publicationDate\":\"2024-07-30\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Journal of Pseudo-Differential Operators and Applications\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s11868-024-00630-1\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Pseudo-Differential Operators and Applications","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s11868-024-00630-1","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

我们研究了封闭黎曼流形上一类包含符号变化项和负幂项的哈代-索博廖方程。借助改进的奈哈里流形方法和一些变分技术，我们确定了正弱解的存在性和多重性，并进行了炸毁行为分析。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

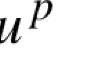
Hardy–Sobolev equation with negative power and sign-changing nonlinearity on closed manifolds

查看原文本刊更多论文

Hardy–Sobolev equation with negative power and sign-changing nonlinearity on closed manifolds

We study a class of Hardy-Sobolev equations containing both sign-changing and negative power terms on closed Riemannian manifolds. With the help of a modified Nehari manifold method and some variational techniques, the existence and multiplicity of positive weak solutions are established, along with blow-up behavior analysis.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Journal of Pseudo-Differential Operators and Applications MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

2.20

自引率

9.10%

发文量

期刊介绍： The Journal of Pseudo-Differential Operators and Applications is a forum for high quality papers in the mathematics, applications and numerical analysis of pseudo-differential operators. Pseudo-differential operators are understood in a very broad sense embracing but not limited to harmonic analysis, functional analysis, operator theory and algebras, partial differential equations, geometry, mathematical physics and novel applications in engineering, geophysics and medical sciences.