有限维李代数上的局部和 2 局部 $$frac{1}{2}$ 衍生
IF 1.2
3区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
在这项工作中,我们引入了局部和二局部 \(\delta \)-derivations的概念,并描述了具有丝状、海森堡和无边际的有限维可解列阵的局部和二局部 \(\frac{1}{2}\)-derivation 。此外,我们还描述了振荡器列阵、薛定谔列阵和具有三维简单部分的列代数的局部 \(\frac{1}{2}\) -衍生,其根是一个不可还原模块。我们证明了一个只有微不足道的(\frac{1}{2}\)derivation的代数不允许局部和2局部的\(\frac{1}{2}\)derivation,这不是\(\frac{1}{2}\)derivation。本文章由计算机程序翻译,如有差异,请以英文原文为准。
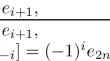
Local and 2-Local $$\frac{1}{2}$$ -Derivations on Finite-Dimensional Lie Algebras
In this work, we introduce the notion of local and 2-local \(\delta \)-derivations and describe local and 2-local \(\frac{1}{2}\)-derivation of finite-dimensional solvable Lie algebras with filiform, Heisenberg, and abelian nilradicals. Moreover, we describe the local \(\frac{1}{2}\)-derivation of oscillator Lie algebras, Schrödinger algebras, and the Lie algebra with the three-dimensional simple part, whose radical is an irreducible module. We prove that an algebra with only trivial \(\frac{1}{2}\)-derivation does not admit local and 2-local \(\frac{1}{2}\)-derivation, which is not \(\frac{1}{2}\)-derivation.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Results in Mathematics
数学-数学
CiteScore
1.90
自引率
4.50%
发文量
198
审稿时长
6-12 weeks
期刊介绍:
Results in Mathematics (RM) publishes mainly research papers in all fields of pure and applied mathematics. In addition, it publishes summaries of any mathematical field and surveys of any mathematical subject provided they are designed to advance some recent mathematical development.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


