模块域内探测器粒子动力学中的金银静止点

IF 0.6 4区数学 Q3 MATHEMATICS

Functional Analysis and Its Applications Pub Date : 2024-07-21 DOI:10.1134/S0016266324020047

Alexander Gorsky, Sergei Nechaev

{"title":"模块域内探测器粒子动力学中的金银静止点","authors":"Alexander Gorsky, Sergei Nechaev","doi":"10.1134/S0016266324020047","DOIUrl":null,"url":null,"abstract":"<p> The flows generated by the iterative dynamics of triangle reflections are analyzed. These flows are interpreted as the adiabatic dynamics of probe particles within the fundamental domain of the modular group. Two specific cases of lattices are considered: (a) those generated by reflections of equilateral triangles, and (b) those generated by reflections of rectangular isosceles triangles. We demonstrate that the stationary points of the flows for equilateral and isosceles triangles correspond to the “Golden” and the “Silver” ratios, respectively. </p>","PeriodicalId":575,"journal":{"name":"Functional Analysis and Its Applications","volume":null,"pages":null},"PeriodicalIF":0.6000,"publicationDate":"2024-07-21","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Golden and Silver Stationary Points in Probe Particle Dynamics within a Modular Domain\",\"authors\":\"Alexander Gorsky, Sergei Nechaev\",\"doi\":\"10.1134/S0016266324020047\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p> The flows generated by the iterative dynamics of triangle reflections are analyzed. These flows are interpreted as the adiabatic dynamics of probe particles within the fundamental domain of the modular group. Two specific cases of lattices are considered: (a) those generated by reflections of equilateral triangles, and (b) those generated by reflections of rectangular isosceles triangles. We demonstrate that the stationary points of the flows for equilateral and isosceles triangles correspond to the “Golden” and the “Silver” ratios, respectively. </p>\",\"PeriodicalId\":575,\"journal\":{\"name\":\"Functional Analysis and Its Applications\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-07-21\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Functional Analysis and Its Applications\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S0016266324020047\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Functional Analysis and Its Applications","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1134/S0016266324020047","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

摘要分析了三角形反射迭代动力学产生的流。这些流被解释为模组基本域内探测粒子的绝热动力学。我们考虑了两种特定的网格情况：(a) 由等边三角形反射产生的网格；(b) 由矩形等腰三角形反射产生的网格。我们证明了等边三角形和等腰三角形的流动静止点分别对应于 "黄金比 "和 "白银比"。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

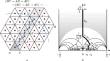
Golden and Silver Stationary Points in Probe Particle Dynamics within a Modular Domain

查看原文本刊更多论文

Golden and Silver Stationary Points in Probe Particle Dynamics within a Modular Domain

The flows generated by the iterative dynamics of triangle reflections are analyzed. These flows are interpreted as the adiabatic dynamics of probe particles within the fundamental domain of the modular group. Two specific cases of lattices are considered: (a) those generated by reflections of equilateral triangles, and (b) those generated by reflections of rectangular isosceles triangles. We demonstrate that the stationary points of the flows for equilateral and isosceles triangles correspond to the “Golden” and the “Silver” ratios, respectively.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Functional Analysis and Its Applications 数学-数学

CiteScore

0.90

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Functional Analysis and Its Applications publishes current problems of functional analysis, including representation theory, theory of abstract and functional spaces, theory of operators, spectral theory, theory of operator equations, and the theory of normed rings. The journal also covers the most important applications of functional analysis in mathematics, mechanics, and theoretical physics.