四边形网格上的二阶收敛不符合多项式斯托克斯元素

IF 2.6 3区数学

Computational and Applied Mathematics Pub Date : 2024-07-13 DOI:10.1007/s40314-024-02842-z

Yuan Bao, Sibo Yang, Zhaoliang Meng, Chaobin Liu, Zhongxuan Luo

{"title":"四边形网格上的二阶收敛不符合多项式斯托克斯元素","authors":"Yuan Bao, Sibo Yang, Zhaoliang Meng, Chaobin Liu, Zhongxuan Luo","doi":"10.1007/s40314-024-02842-z","DOIUrl":null,"url":null,"abstract":"In this paper, we construct a new mixed finite element for the Stokes problem on general convex quadrilateral partitions. The velocity is approximated by piecewise polynomial element space, and the pressure is approximated by piecewise constant. Moreover, we assert that the discrete velocity is second-order convergent in discrete \\(H^{1}\\) seminorm, and the convergence order of the pressure solution can be improved to second by a post-processing for Stokes problems. Lastly, numerical tests verify the convergence analysis.","PeriodicalId":51278,"journal":{"name":"Computational and Applied Mathematics","volume":"7 1","pages":""},"PeriodicalIF":2.6000,"publicationDate":"2024-07-13","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"A second-order convergent nonconforming polynomial stokes element on quadrilateral meshes\",\"authors\":\"Yuan Bao, Sibo Yang, Zhaoliang Meng, Chaobin Liu, Zhongxuan Luo\",\"doi\":\"10.1007/s40314-024-02842-z\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we construct a new mixed finite element for the Stokes problem on general convex quadrilateral partitions. The velocity is approximated by piecewise polynomial element space, and the pressure is approximated by piecewise constant. Moreover, we assert that the discrete velocity is second-order convergent in discrete \\\\(H^{1}\\\\) seminorm, and the convergence order of the pressure solution can be improved to second by a post-processing for Stokes problems. Lastly, numerical tests verify the convergence analysis.\",\"PeriodicalId\":51278,\"journal\":{\"name\":\"Computational and Applied Mathematics\",\"volume\":\"7 1\",\"pages\":\"\"},\"PeriodicalIF\":2.6000,\"publicationDate\":\"2024-07-13\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Computational and Applied Mathematics\",\"FirstCategoryId\":\"1085\",\"ListUrlMain\":\"https://doi.org/10.1007/s40314-024-02842-z\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"\",\"JCRName\":\"\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Computational and Applied Mathematics","FirstCategoryId":"1085","ListUrlMain":"https://doi.org/10.1007/s40314-024-02842-z","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"","JCRName":"","Score":null,"Total":0}

引用次数: 0

摘要

本文为一般凸四边形分区上的斯托克斯问题构建了一种新的混合有限元。速度用分段多项式元素空间逼近，压力用分段常数逼近。此外，我们断言离散速度在离散 \(H^{1}\) 半规范下是二阶收敛的，压力解的收敛阶数可以通过斯托克斯问题的后处理提高到二阶。最后，数值试验验证了收敛分析。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

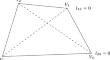
A second-order convergent nonconforming polynomial stokes element on quadrilateral meshes

查看原文本刊更多论文

A second-order convergent nonconforming polynomial stokes element on quadrilateral meshes

In this paper, we construct a new mixed finite element for the Stokes problem on general convex quadrilateral partitions. The velocity is approximated by piecewise polynomial element space, and the pressure is approximated by piecewise constant. Moreover, we assert that the discrete velocity is second-order convergent in discrete \(H^{1}\) seminorm, and the convergence order of the pressure solution can be improved to second by a post-processing for Stokes problems. Lastly, numerical tests verify the convergence analysis.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Computational and Applied Mathematics MATHEMATICS, APPLIED-

自引率

11.50%

发文量

352

期刊介绍： Computational & Applied Mathematics began to be published in 1981. This journal was conceived as the main scientific publication of SBMAC (Brazilian Society of Computational and Applied Mathematics). The objective of the journal is the publication of original research in Applied and Computational Mathematics, with interfaces in Physics, Engineering, Chemistry, Biology, Operations Research, Statistics, Social Sciences and Economy. The journal has the usual quality standards of scientific international journals and we aim high level of contributions in terms of originality, depth and relevance.