非ermitian 带中拓扑非阿贝尔辫状结构的无监督学习
IF 18.8
1区 计算机科学
Q1 COMPUTER SCIENCE, ARTIFICIAL INTELLIGENCE
引用次数: 0
摘要
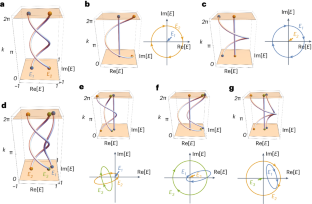
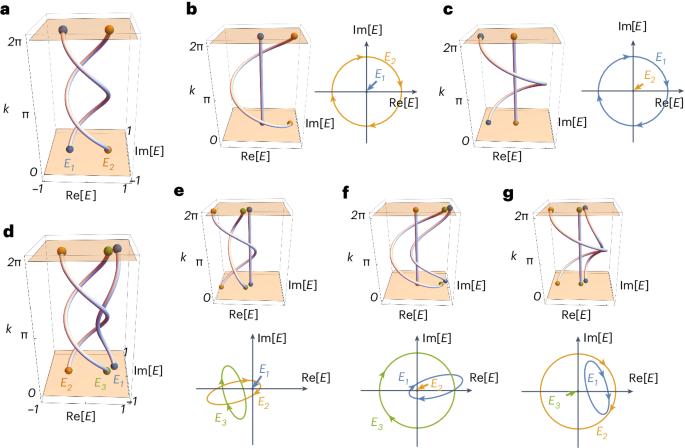
近几十年来,能带的拓扑分类为发现物质的各种拓扑阶段奠定了基础。以前的工作主要集中在赫米特系统中的实能带,而最近的研究则把注意力转移到了复能带或非赫米特能带的奇妙拓扑学上,使它们摆脱了能量守恒的限制。例如,复能带的谱绕组可以产生独特的拓扑结构,如辫状结构,为推进量子计算带来了巨大希望。然而,关于复能辫状结构的讨论主要局限于阿贝尔辫状结构群({{\mathbb{B}}}_{2}\),因为它相对简单。识别拓扑非阿贝尔辫状结构仍然具有挑战性,因为它缺乏普遍适用的拓扑不变量来表征。在这里,我们提出了一种机器学习算法,用于在多个复能带内无监督地识别非阿贝尔辫状结构。我们证明了这一结果与阿尔廷著名的辫状拓扑等价条件是一致的。受这些发现的启发,我们引入了缠绕矩阵作为表征辫状拓扑的拓扑不变量。缠绕矩阵还揭示了非赫米带与非阿贝尔辫状结构的体边对应关系。最后,我们扩展了我们的方法,以识别二维和三维非凡半金属中的非阿贝尔编织拓扑,并以无监督的方式解决解结问题。本文章由计算机程序翻译,如有差异,请以英文原文为准。
Unsupervised learning of topological non-Abelian braiding in non-Hermitian bands
The topological classification of energy bands has laid the foundation for the discovery of various topological phases of matter in recent decades. While previous work focused on real-energy bands in Hermitian systems, recent studies have shifted attention to the intriguing topology of complex-energy, or non-Hermitian, bands, freeing them from the constraint of energy conservation. For example, the spectral winding of complex-energy bands can give rise to unique topological structures such as braids, holding substantial promise for advancing quantum computing. However, discussions of complex-energy braids have been predominantly limited to the Abelian braid group $${{\mathbb{B}}}_{2}$$ owing to its relative simplicity. Identifying topological non-Abelian braiding remains challenging, as it lacks a universally applicable topological invariant for characterization. Here we present a machine learning algorithm for the unsupervised identification of non-Abelian braiding within multiple complex-energy bands. We demonstrate that the results are consistent with Artin’s well-known topological equivalence conditions in braiding. Inspired by these findings, we introduce a winding matrix as a topological invariant for characterizing braiding topology. The winding matrix also reveals the bulk-edge correspondence of non-Hermitian bands with non-Abelian braiding. Finally, we extend our approach to identify non-Abelian braiding topology in two-dimensional and three-dimensional exceptional semimetals and address the unknotting problem in an unsupervised manner. The topological classification of complex-energy bands has uncovered various topological phases beyond Hermitian systems. Long and colleagues exploit unsupervised learning to fully identify the non-Abelian braiding topology of non-Hermitian bands.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Nature Machine Intelligence
Multiple-
CiteScore
36.90
自引率
2.10%
发文量
127
期刊介绍:
Nature Machine Intelligence is a distinguished publication that presents original research and reviews on various topics in machine learning, robotics, and AI. Our focus extends beyond these fields, exploring their profound impact on other scientific disciplines, as well as societal and industrial aspects. We recognize limitless possibilities wherein machine intelligence can augment human capabilities and knowledge in domains like scientific exploration, healthcare, medical diagnostics, and the creation of safe and sustainable cities, transportation, and agriculture. Simultaneously, we acknowledge the emergence of ethical, social, and legal concerns due to the rapid pace of advancements.
To foster interdisciplinary discussions on these far-reaching implications, Nature Machine Intelligence serves as a platform for dialogue facilitated through Comments, News Features, News & Views articles, and Correspondence. Our goal is to encourage a comprehensive examination of these subjects.
Similar to all Nature-branded journals, Nature Machine Intelligence operates under the guidance of a team of skilled editors. We adhere to a fair and rigorous peer-review process, ensuring high standards of copy-editing and production, swift publication, and editorial independence.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


