通过林-路-尤曲率限定完全规则图的直径和特征值
IF 1
2区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
一个充裕正则图是这样一个正则图:任意两个相邻的顶点都有\(\alpha \)个共同的邻接点,任意两个距离为2的顶点都有\(\beta \)个共同的邻接点。我们证明了任何周长为 3 和 \(\beta >\alpha \) 的充分规则图的林-卢-尤曲率的一个尖锐的下界估计值。证明涉及离散里奇曲率与局部匹配特性相关的新想法:这包括从局部结构和相关的距离估计中构造出一个规则的二方图。因此,我们得到了充分规则图的尖锐直径和特征值边界。本文章由计算机程序翻译,如有差异,请以英文原文为准。
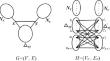
Bounding the Diameter and Eigenvalues of Amply Regular Graphs via Lin–Lu–Yau Curvature
An amply regular graph is a regular graph such that any two adjacent vertices have \(\alpha \) common neighbors and any two vertices with distance 2 have \(\beta \) common neighbors. We prove a sharp lower bound estimate for the Lin–Lu–Yau curvature of any amply regular graph with girth 3 and \(\beta >\alpha \). The proof involves new ideas relating discrete Ricci curvature with local matching properties: This includes a novel construction of a regular bipartite graph from the local structure and related distance estimates. As a consequence, we obtain sharp diameter and eigenvalue bounds for amply regular graphs.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Combinatorica
数学-数学
CiteScore
1.90
自引率
0.00%
发文量
45
审稿时长
>12 weeks
期刊介绍:
COMBINATORICA publishes research papers in English in a variety of areas of combinatorics and the theory of computing, with particular emphasis on general techniques and unifying principles. Typical but not exclusive topics covered by COMBINATORICA are
- Combinatorial structures (graphs, hypergraphs, matroids, designs, permutation groups).
- Combinatorial optimization.
- Combinatorial aspects of geometry and number theory.
- Algorithms in combinatorics and related fields.
- Computational complexity theory.
- Randomization and explicit construction in combinatorics and algorithms.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


