拉普拉奇特征映射的收敛性及其对具有奇点的子实体的收敛率

IF 0.6 3区数学 Q4 COMPUTER SCIENCE, THEORY & METHODS

Discrete & Computational Geometry Pub Date : 2024-07-02 DOI:10.1007/s00454-024-00667-5

Masayuki Aino

{"title":"拉普拉奇特征映射的收敛性及其对具有奇点的子实体的收敛率","authors":"Masayuki Aino","doi":"10.1007/s00454-024-00667-5","DOIUrl":null,"url":null,"abstract":"In this paper, we give a spectral approximation result for the Laplacian on submanifolds of Euclidean spaces with singularities by the \\(\\epsilon \\)-neighborhood graph constructed from random points on the submanifold. Our convergence rate for the eigenvalue of the Laplacian is \\(O\\left( \\left( \\log n/n\\right) ^{1/(m+2)}\\right) \\), where m and n denote the dimension of the manifold and the sample size, respectively.","PeriodicalId":50574,"journal":{"name":"Discrete & Computational Geometry","volume":"131 1","pages":""},"PeriodicalIF":0.6000,"publicationDate":"2024-07-02","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Convergence of Laplacian Eigenmaps and Its Rate for Submanifolds with Singularities\",\"authors\":\"Masayuki Aino\",\"doi\":\"10.1007/s00454-024-00667-5\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we give a spectral approximation result for the Laplacian on submanifolds of Euclidean spaces with singularities by the \\\\(\\\\epsilon \\\\)-neighborhood graph constructed from random points on the submanifold. Our convergence rate for the eigenvalue of the Laplacian is \\\\(O\\\\left( \\\\left( \\\\log n/n\\\\right) ^{1/(m+2)}\\\\right) \\\\), where m and n denote the dimension of the manifold and the sample size, respectively.\",\"PeriodicalId\":50574,\"journal\":{\"name\":\"Discrete & Computational Geometry\",\"volume\":\"131 1\",\"pages\":\"\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-07-02\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Discrete & Computational Geometry\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00454-024-00667-5\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q4\",\"JCRName\":\"COMPUTER SCIENCE, THEORY & METHODS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Discrete & Computational Geometry","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00454-024-00667-5","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q4","JCRName":"COMPUTER SCIENCE, THEORY & METHODS","Score":null,"Total":0}

引用次数: 0

摘要

在本文中，我们给出了欧几里得空间具有奇点的子曼形上的拉普拉斯函数的谱近似结果，即通过子曼形上的随机点构建的（\epsilon \）邻域图。我们对拉普拉斯函数特征值的收敛率是\(O\left( \left( \log n/n\right) ^{1/(m+2)}\right) \)，其中m和n分别表示流形的维数和样本大小。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

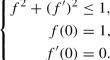
Convergence of Laplacian Eigenmaps and Its Rate for Submanifolds with Singularities

查看原文本刊更多论文

Convergence of Laplacian Eigenmaps and Its Rate for Submanifolds with Singularities

In this paper, we give a spectral approximation result for the Laplacian on submanifolds of Euclidean spaces with singularities by the \(\epsilon \)-neighborhood graph constructed from random points on the submanifold. Our convergence rate for the eigenvalue of the Laplacian is \(O\left( \left( \log n/n\right) ^{1/(m+2)}\right) \), where m and n denote the dimension of the manifold and the sample size, respectively.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Discrete & Computational Geometry 数学-计算机：理论方法

CiteScore

1.80

自引率

12.50%

发文量

审稿时长

6-12 weeks

期刊介绍： Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.