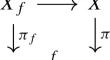
Non-thin rank jumps for double elliptic K3 surfaces

For an elliptic surface \(\pi :X\rightarrow \mathbb {P}^1\) defined over a number field K, a theorem of Silverman shows that for all but finitely many fibres above K-rational points, the resulting elliptic curve over K has Mordell-Weil rank at least as large as the rank of the group of sections of \(\pi \). When X is a K3 surface with two distinct elliptic fibrations, we show that the set of K-rational points of \(\mathbb {P}^1\) for which this rank inequality is strict, is not a thin set, under certain hypothesis on the fibrations. Our results provide one of the first cases of this phenomenon beyond that of rational elliptic surfaces.