沉浸于萨萨克空间形式
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
我们研究萨萨基流形对有限维和无限维萨萨基空间形式的浸入。在证明了卡拉比在萨萨基元环境中的刚性结果之后,我们描述了所有允许(局部)萨萨基元浸入非椭圆萨萨基元空间形式的均质萨萨基元流形的特征。此外,我们还给出了在紧凑和非紧凑情况下都能嵌入标准球的均质萨萨流形的特征。本文章由计算机程序翻译,如有差异,请以英文原文为准。
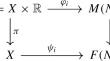
Immersions into Sasakian space forms
We study immersions of Sasakian manifolds into finite and infinite dimensional Sasakian space forms. After proving Calabi’s rigidity results in the Sasakian setting, we characterise all homogeneous Sasakian manifolds which admit a (local) Sasakian immersion into a nonelliptic Sasakian space form. Moreover, we give a characterisation of homogeneous Sasakian manifolds which can be embedded into the standard sphere both in the compact and noncompact case.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


