N 稳定类别
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
布赫维茨(Buchweitz)的一个著名定理提供了三个范畴之间的等价性:戈伦斯坦代数上的戈伦斯坦射影模块的稳定范畴、射影无环复数的同调范畴和奇点范畴。为了将这一结果应用于 N 复数,我们必须为稳定范畴的 N 类似范畴找到一个合适的候选范畴。我们通过单态范畴确定了这个 "N-稳定范畴",并证明了布赫维茨关于格罗内迪克阿贝尔范畴上 N-复数的定理。我们还计算了在自注入代数上的 N-稳定范畴的 Serre 函数,并研究了由此产生的分数 Calabi-Yau 属性。本文章由计算机程序翻译,如有差异,请以英文原文为准。
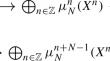
The N-stable category
A well-known theorem of Buchweitz provides equivalences between three categories: the stable category of Gorenstein projective modules over a Gorenstein algebra, the homotopy category of acyclic complexes of projectives, and the singularity category. To adapt this result to N-complexes, one must find an appropriate candidate for the N-analogue of the stable category. We identify this “N-stable category” via the monomorphism category and prove Buchweitz’s theorem for N-complexes over a Grothendieck abelian category. We also compute the Serre functor on the N-stable category over a self-injective algebra and study the resultant fractional Calabi–Yau properties.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


