具有多个独立顶点切分的图形

IF 0.6 4区数学 Q3 MATHEMATICS

Graphs and Combinatorics Pub Date : 2024-06-25 DOI:10.1007/s00373-024-02811-7

Yanan Hu, Xingzhi Zhan, Leilei Zhang

{"title":"具有多个独立顶点切分的图形","authors":"Yanan Hu, Xingzhi Zhan, Leilei Zhang","doi":"10.1007/s00373-024-02811-7","DOIUrl":null,"url":null,"abstract":"Cycles are the only 2-connected graphs in which any two nonadjacent vertices form a vertex cut. We generalize this fact by proving that for every integer \\(k\\ge 3\\) there exists a unique graph G satisfying the following three conditions: (1) G is k-connected; (2) the independence number of G is greater than k; (3) any independent set of cardinality k is a vertex cut of G. However, the edge version of this result does not hold. We also consider the problem when replacing independent sets by the periphery.","PeriodicalId":12811,"journal":{"name":"Graphs and Combinatorics","volume":null,"pages":null},"PeriodicalIF":0.6000,"publicationDate":"2024-06-25","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Graphs with Many Independent Vertex Cuts\",\"authors\":\"Yanan Hu, Xingzhi Zhan, Leilei Zhang\",\"doi\":\"10.1007/s00373-024-02811-7\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"Cycles are the only 2-connected graphs in which any two nonadjacent vertices form a vertex cut. We generalize this fact by proving that for every integer \\\\(k\\\\ge 3\\\\) there exists a unique graph G satisfying the following three conditions: (1) G is k-connected; (2) the independence number of G is greater than k; (3) any independent set of cardinality k is a vertex cut of G. However, the edge version of this result does not hold. We also consider the problem when replacing independent sets by the periphery.\",\"PeriodicalId\":12811,\"journal\":{\"name\":\"Graphs and Combinatorics\",\"volume\":null,\"pages\":null},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-06-25\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Graphs and Combinatorics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00373-024-02811-7\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Graphs and Combinatorics","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00373-024-02811-7","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

循环是唯一两个不相邻的顶点形成一个顶点切口的 2 连接图。我们通过证明对于每一个整数（k\ge 3\）都存在一个满足以下三个条件的唯一图 G 来推广这一事实：（1）G 是 k 连接的；（2）G 的独立数大于 k；（3）任何心率为 k 的独立集都是 G 的顶点切分。我们还考虑了用边缘代替独立集的问题。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

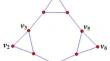
Graphs with Many Independent Vertex Cuts

查看原文本刊更多论文

Graphs with Many Independent Vertex Cuts

Cycles are the only 2-connected graphs in which any two nonadjacent vertices form a vertex cut. We generalize this fact by proving that for every integer \(k\ge 3\) there exists a unique graph G satisfying the following three conditions: (1) G is k-connected; (2) the independence number of G is greater than k; (3) any independent set of cardinality k is a vertex cut of G. However, the edge version of this result does not hold. We also consider the problem when replacing independent sets by the periphery.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Graphs and Combinatorics 数学-数学

CiteScore

1.00

自引率

14.30%

发文量

160

审稿时长

6 months

期刊介绍： Graphs and Combinatorics is an international journal devoted to research concerning all aspects of combinatorial mathematics. In addition to original research papers, the journal also features survey articles from authors invited by the editorial board.