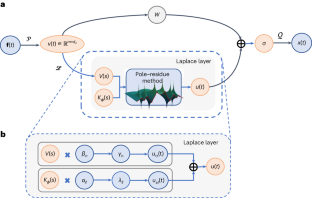
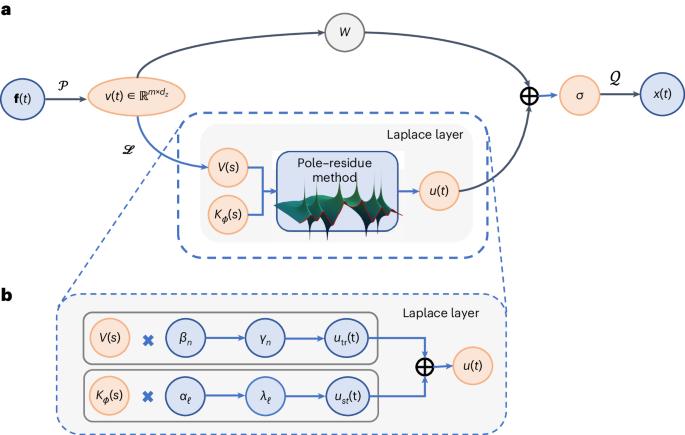
Laplace neural operator for solving differential equations

Neural operators map multiple functions to different functions, possibly in different spaces, unlike standard neural networks. Hence, neural operators allow the solution of parametric ordinary differential equations (ODEs) and partial differential equations (PDEs) for a distribution of boundary or initial conditions and excitations, but can also be used for system identification as well as designing various components of digital twins. We introduce the Laplace neural operator (LNO), which incorporates the pole–residue relationship between input–output spaces, leading to better interpretability and generalization for certain classes of problems. The LNO is capable of processing non-periodic signals and transient responses resulting from simultaneously zero and non-zero initial conditions, which makes it achieve better approximation accuracy over other neural operators for extrapolation circumstances in solving several ODEs and PDEs. We also highlight the LNO’s good interpolation ability, from a low-resolution input to high-resolution outputs at arbitrary locations within the domain. To demonstrate the scalability of LNO, we conduct large-scale simulations of Rossby waves around the globe, employing millions of degrees of freedom. Taken together, our findings show that a pretrained LNO model offers an effective real-time solution for general ODEs and PDEs at scale and is an efficient alternative to existing neural operators. Neural operators are powerful neural networks that approximate nonlinear dynamical systems and their responses. Cao and colleagues introduce the Laplace neural operator, a scalable approach that can effectively deal with non-periodic signals and transient responses and can outperform existing neural operators on certain classes of ODE and PDE problems.