沃罗诺伊路径和景观的平均失真和预期失真
IF 0.6
3区 数学
Q4 COMPUTER SCIENCE, THEORY & METHODS
引用次数: 0
摘要
用精细正方形网格的边缘近似一个圆时,其周长的扭曲系数约为\(\tfrac{4}{pi }\) 。我们证明,对于用任何非奇异的 Delaunay 马赛克(被称为 Voronoi 路径)的边缘逼近任何可整型曲线,这个因子的平均值是相同的(在遍历意义上),并将结果扩展到所有维度,将 Voronoi 路径推广到 Voronoi Scapes。本文章由计算机程序翻译,如有差异,请以英文原文为准。
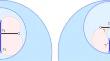
Average and Expected Distortion of Voronoi Paths and Scapes
The approximation of a circle with the edges of a fine square grid distorts the perimeter by a factor about \(\tfrac{4}{\pi }\). We prove that this factor is the same on average (in the ergodic sense) for approximations of any rectifiable curve by the edges of any non-exotic Delaunay mosaic (known as Voronoi path), and extend the results to all dimensions, generalizing Voronoi paths to Voronoi scapes.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Discrete & Computational Geometry
数学-计算机:理论方法
CiteScore
1.80
自引率
12.50%
发文量
99
审稿时长
6-12 weeks
期刊介绍:
Discrete & Computational Geometry (DCG) is an international journal of mathematics and computer science, covering a broad range of topics in which geometry plays a fundamental role. It publishes papers on such topics as configurations and arrangements, spatial subdivision, packing, covering, and tiling, geometric complexity, polytopes, point location, geometric probability, geometric range searching, combinatorial and computational topology, probabilistic techniques in computational geometry, geometric graphs, geometry of numbers, and motion planning.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


