论二阶线性微分方程的无限 $$\varphi $$ 阶解

IF 0.6 4区数学 Q3 MATHEMATICS

Computational Methods and Function Theory Pub Date : 2024-05-29 DOI:10.1007/s40315-024-00548-1

Hui Yu, Xiaomin Li

{"title":"论二阶线性微分方程的无限 $$\\varphi $$ 阶解","authors":"Hui Yu, Xiaomin Li","doi":"10.1007/s40315-024-00548-1","DOIUrl":null,"url":null,"abstract":"In this paper, we consider the second order linear differential equation where A, B and F with \$B\\not \\equiv 0\$ are entire functions. We find some appropriate conditions on A, B and F in terms of the \$\\varphi \$-order which guarantee that every non-constant entire solution f of (†) has infinite \$\\varphi \$-order, along with an additional relation between the hyper-\$\\varphi \$-order of f and the \$\\varphi \$-order of the dominating coefficient in (†).","PeriodicalId":49088,"journal":{"name":"Computational Methods and Function Theory","volume":"11 7 1","pages":""},"PeriodicalIF":0.6000,"publicationDate":"2024-05-29","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"On the Infinite $$\\\\varphi $$ -Order Solutions of Second Order Linear Differential Equations\",\"authors\":\"Hui Yu, Xiaomin Li\",\"doi\":\"10.1007/s40315-024-00548-1\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In this paper, we consider the second order linear differential equation where A, B and F with \\\$B\\\\not \\\\equiv 0\\\$ are entire functions. We find some appropriate conditions on A, B and F in terms of the \\\$\\\\varphi \\\$-order which guarantee that every non-constant entire solution f of (†) has infinite \\\$\\\\varphi \\\$-order, along with an additional relation between the hyper-\\\$\\\\varphi \\\$-order of f and the \\\$\\\\varphi \\\$-order of the dominating coefficient in (†).\",\"PeriodicalId\":49088,\"journal\":{\"name\":\"Computational Methods and Function Theory\",\"volume\":\"11 7 1\",\"pages\":\"\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-05-29\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Computational Methods and Function Theory\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s40315-024-00548-1\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Computational Methods and Function Theory","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s40315-024-00548-1","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

在本文中，我们考虑了二阶线性微分方程，其中 A、B 和 F 都是$B\not \equiv 0$ 全函数。我们从 $\varphi $-阶的角度找到了一些关于 A、B 和 F 的适当条件，这些条件保证了 (†) 的每个非常数全解 f 具有无限的 $\varphi $-阶，同时还找到了 f 的超 $\varphi $-阶与 (†) 中支配系数的 $\varphi $-阶之间的附加关系。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

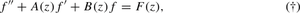
$On the Infinite $$\varphi $$ -Order Solutions of Second Order Linear Differential Equations$

查看原文本刊更多论文

On the Infinite $$\varphi $$ -Order Solutions of Second Order Linear Differential Equations

In this paper, we consider the second order linear differential equation

where A, B and F with $B\not \equiv 0$ are entire functions. We find some appropriate conditions on A, B and F in terms of the $\varphi $-order which guarantee that every non-constant entire solution f of (†) has infinite $\varphi $-order, along with an additional relation between the hyper-$\varphi $-order of f and the $\varphi $-order of the dominating coefficient in (†).

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Computational Methods and Function Theory MATHEMATICS, APPLIED-MATHEMATICS

CiteScore

3.20

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： CMFT is an international mathematics journal which publishes carefully selected original research papers in complex analysis (in a broad sense), and on applications or computational methods related to complex analysis. Survey articles of high standard and current interest can be considered for publication as well.