解决非 Lipschitz 算子的变分不等式问题的修正投影法和强收敛定理

IF 1.7 3区数学 Q2 MATHEMATICS, APPLIED

Numerical Algorithms Pub Date : 2024-06-01 DOI:10.1007/s11075-024-01851-7

Zhongbing Xie, Huanqin Wu, Liya Liu

{"title":"解决非 Lipschitz 算子的变分不等式问题的修正投影法和强收敛定理","authors":"Zhongbing Xie, Huanqin Wu, Liya Liu","doi":"10.1007/s11075-024-01851-7","DOIUrl":null,"url":null,"abstract":"<p>In this paper, we introduce a modified projection method and give a strong convergence theorem for solving variational inequality problems in real Hilbert spaces. Under mild assumptions, there exists a novel line-search rule that makes the proposed algorithm suitable for non-Lipschitz continuous and pseudo-monotone operators. Compared with other known algorithms in numerical experiments, it is shown that our algorithm has better numerical performance.</p>","PeriodicalId":54709,"journal":{"name":"Numerical Algorithms","volume":"31 1","pages":""},"PeriodicalIF":1.7000,"publicationDate":"2024-06-01","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Modified projection method and strong convergence theorem for solving variational inequality problems with non-Lipschitz operators\",\"authors\":\"Zhongbing Xie, Huanqin Wu, Liya Liu\",\"doi\":\"10.1007/s11075-024-01851-7\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>In this paper, we introduce a modified projection method and give a strong convergence theorem for solving variational inequality problems in real Hilbert spaces. Under mild assumptions, there exists a novel line-search rule that makes the proposed algorithm suitable for non-Lipschitz continuous and pseudo-monotone operators. Compared with other known algorithms in numerical experiments, it is shown that our algorithm has better numerical performance.</p>\",\"PeriodicalId\":54709,\"journal\":{\"name\":\"Numerical Algorithms\",\"volume\":\"31 1\",\"pages\":\"\"},\"PeriodicalIF\":1.7000,\"publicationDate\":\"2024-06-01\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Numerical Algorithms\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s11075-024-01851-7\",\"RegionNum\":3,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q2\",\"JCRName\":\"MATHEMATICS, APPLIED\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Numerical Algorithms","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s11075-024-01851-7","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS, APPLIED","Score":null,"Total":0}

引用次数: 0

摘要

本文介绍了一种改进的投影法，并给出了求解实希尔伯特空间中变不等式问题的强收敛定理。在温和的假设条件下，存在一种新颖的线性搜索规则，使得所提出的算法适用于非 Lipschitz 连续和伪单调算子。数值实验表明，与其他已知算法相比，我们的算法具有更好的数值性能。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

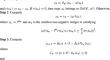
Modified projection method and strong convergence theorem for solving variational inequality problems with non-Lipschitz operators

查看原文本刊更多论文

Modified projection method and strong convergence theorem for solving variational inequality problems with non-Lipschitz operators

In this paper, we introduce a modified projection method and give a strong convergence theorem for solving variational inequality problems in real Hilbert spaces. Under mild assumptions, there exists a novel line-search rule that makes the proposed algorithm suitable for non-Lipschitz continuous and pseudo-monotone operators. Compared with other known algorithms in numerical experiments, it is shown that our algorithm has better numerical performance.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Numerical Algorithms 数学-应用数学

CiteScore

4.00

自引率

9.50%

发文量

201

审稿时长

9 months

期刊介绍： The journal Numerical Algorithms is devoted to numerical algorithms. It publishes original and review papers on all the aspects of numerical algorithms: new algorithms, theoretical results, implementation, numerical stability, complexity, parallel computing, subroutines, and applications. Papers on computer algebra related to obtaining numerical results will also be considered. It is intended to publish only high quality papers containing material not published elsewhere.