分数色度数的 Schrijver 图临界子图

IF 0.6 4区数学 Q3 MATHEMATICS

Graphs and Combinatorics Pub Date : 2024-05-10 DOI:10.1007/s00373-024-02782-9

Anna Gujgiczer, Gábor Simonyi

{"title":"分数色度数的 Schrijver 图临界子图","authors":"Anna Gujgiczer, Gábor Simonyi","doi":"10.1007/s00373-024-02782-9","DOIUrl":null,"url":null,"abstract":"<p>Schrijver graphs are vertex-color-critical subgraphs of Kneser graphs having the same chromatic number. They also share the value of their fractional chromatic number but Schrijver graphs are not critical for that. Here we present an induced subgraph of every Schrijver graph that is vertex-critical with respect to the fractional chromatic number. These subgraphs turn out to be isomorphic with certain circular complete graphs. We also characterize the critical edges within this subgraph.</p>","PeriodicalId":12811,"journal":{"name":"Graphs and Combinatorics","volume":"40 1","pages":""},"PeriodicalIF":0.6000,"publicationDate":"2024-05-10","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"Critical Subgraphs of Schrijver Graphs for the Fractional Chromatic Number\",\"authors\":\"Anna Gujgiczer, Gábor Simonyi\",\"doi\":\"10.1007/s00373-024-02782-9\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"<p>Schrijver graphs are vertex-color-critical subgraphs of Kneser graphs having the same chromatic number. They also share the value of their fractional chromatic number but Schrijver graphs are not critical for that. Here we present an induced subgraph of every Schrijver graph that is vertex-critical with respect to the fractional chromatic number. These subgraphs turn out to be isomorphic with certain circular complete graphs. We also characterize the critical edges within this subgraph.</p>\",\"PeriodicalId\":12811,\"journal\":{\"name\":\"Graphs and Combinatorics\",\"volume\":\"40 1\",\"pages\":\"\"},\"PeriodicalIF\":0.6000,\"publicationDate\":\"2024-05-10\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Graphs and Combinatorics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://doi.org/10.1007/s00373-024-02782-9\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Graphs and Combinatorics","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1007/s00373-024-02782-9","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

Schrijver 图是具有相同色度数的 Kneser 图的顶点颜色临界子图。它们还共享分数色度数的值，但 Schrijver 图对此并不关键。在这里，我们提出了每个 Schrijver 图的诱导子图，这些子图在小数色度数方面都是顶点临界图。这些子图与某些圆形完整图同构。我们还描述了该子图中临界边的特征。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

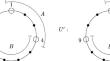
Critical Subgraphs of Schrijver Graphs for the Fractional Chromatic Number

查看原文本刊更多论文

Critical Subgraphs of Schrijver Graphs for the Fractional Chromatic Number

Schrijver graphs are vertex-color-critical subgraphs of Kneser graphs having the same chromatic number. They also share the value of their fractional chromatic number but Schrijver graphs are not critical for that. Here we present an induced subgraph of every Schrijver graph that is vertex-critical with respect to the fractional chromatic number. These subgraphs turn out to be isomorphic with certain circular complete graphs. We also characterize the critical edges within this subgraph.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Graphs and Combinatorics 数学-数学

CiteScore

1.00

自引率

14.30%

发文量

160

审稿时长

6 months

期刊介绍： Graphs and Combinatorics is an international journal devoted to research concerning all aspects of combinatorial mathematics. In addition to original research papers, the journal also features survey articles from authors invited by the editorial board.