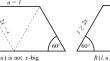
Perfectly Packing an Equilateral Triangle by Equilateral Triangles of Sidelengths $$n^{-1/2-\epsilon }$$

Equilateral triangles of sidelengths 1, \(2^{-t}\), \(3^{-t}\), \(4^{-t},\ldots \ \) can be packed perfectly into an equilateral triangle, provided that \(\ 1/2<t \le 37/72\). Moreover, for t slightly greater than 1/2, squares of sidelengths 1, \(2^{-t}\), \(3^{-t}\), \(4^{-t},\ldots \ \) can be packed perfectly into a square \(S_t\) in such a way that some squares have a side parallel to a diagonal of \(S_t\) and the remaining squares have a side parallel to a side of \(S_t\).