海森堡群上开普勒问题的动力学原理
IF 1.4
3区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
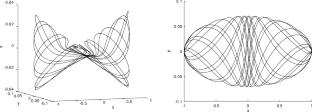
我们研究的是海森堡群上的一个点粒子围绕固定在原点的 "太阳 "的非全局运动,而 "太阳 "的势能是由子拉普拉斯的基本解给出的。最近有几篇论文将这一问题视为变分问题(因此是控制问题),与此相反,我们研究的是非荷尔蒙力学中的非变分动力运动方程。我们找到了该系统的三个独立的第一次积分,并证明其有界轨迹是围绕某些四阶曲面展开的。我们还描述了轨迹的一些特殊情况。本文章由计算机程序翻译,如有差异,请以英文原文为准。
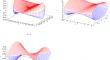
Dynamics in the Kepler problem on the Heisenberg group
We study the nonholonomic motion of a point particle on the Heisenberg group around the fixed “sun” placed at the origin whose potential is given by the fundamental solution of the sub-Laplacian. In contrast with several recent papers that approach this problem as a variational one (hence a control problem) we study the equations of dynamical motion which are non-variational in nonholonomic mechanics. We find three independent first integrals of the system and show that its bounded trajectories are wound up around certain surfaces of the fourth order. We also describe some particular cases of trajectories.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Analysis and Mathematical Physics
MATHEMATICS, APPLIED-MATHEMATICS
CiteScore
2.70
自引率
0.00%
发文量
122
期刊介绍:
Analysis and Mathematical Physics (AMP) publishes current research results as well as selected high-quality survey articles in real, complex, harmonic; and geometric analysis originating and or having applications in mathematical physics. The journal promotes dialog among specialists in these areas.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


