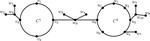
The doubly metric dimensions of cactus graphs and block graphs

Given a connected graph G, two vertices \(u,v\in V(G)\) doubly resolve \(x,y\in V(G)\) if \(d_{G}(x,u)-d_{G}(y,u)\ne d_{G}(x,v)-d_{G}(y,v)\). The doubly metric dimension \(\psi (G)\) of G is the cardinality of a minimum set of vertices that doubly resolves each pair of vertices from V(G). It is well known that deciding the doubly metric dimension of G is NP-hard. In this work we determine the exact values of doubly metric dimensions of unicyclic graphs which completes the known result. Furthermore, we give formulae for doubly metric dimensions of cactus graphs and block graphs.