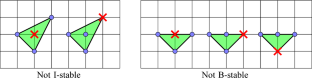
Triangle Percolation on the Grid

We consider a geometric percolation process partially motivated by recent work of Hejda and Kala. Specifically, we start with an initial set \(X \subseteq {\mathbb {Z}}^2\), and then iteratively check whether there exists a triangle \(T \subseteq {\mathbb {R}}^2\) with its vertices in \({\mathbb {Z}}^2\) such that T contains exactly four points of \({\mathbb {Z}}^2\) and exactly three points of X. In this case, we add the missing lattice point of T to X, and we repeat until no such triangle exists. We study the limit sets S, the sets stable under this process, including determining their possible densities and some of their structure.