两区间片断仿射映射的旋转数
IF 0.9
3区 数学
Q2 MATHEMATICS
引用次数: 0
摘要
我们研究单位区间的映射,这些映射的图是由两个递增段组成的,并且在扩展意义上是注入的。这种映射的参数是满足不等式的实数五元组 \(\varvec{p}}\)。把 \(f_{varvec{p}} 看作一个圆图,我们证明它有一个旋转数 \(\rho (f_{varvec{p}}) \),我们用赫克-马勒数列计算 \(\rho (f_{varvec{p}}) \)作为 \(\varvec{p}}) 的函数。作为推论,我们证明当 \(\varvec{p}) 的分量是代数数时,\(\rho (f_{\varvec{p}}) 是有理数。本文章由计算机程序翻译,如有差异,请以英文原文为准。
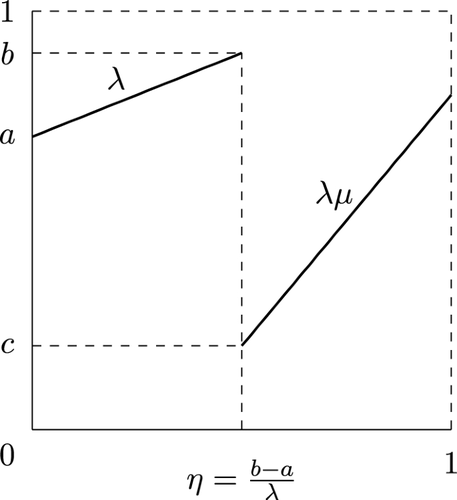
Rotation number of 2-interval piecewise affine maps
We study maps of the unit interval whose graph is made up of two increasing segments and which are injective in an extended sense. Such maps \(f_{\varvec{p}}\) are parametrized by a quintuple \(\varvec{p}\) of real numbers satisfying inequations. Viewing \(f_{\varvec{p}}\) as a circle map, we show that it has a rotation number \(\rho (f_{\varvec{p}})\) and we compute \(\rho (f_{\varvec{p}})\) as a function of \(\varvec{p}\) in terms of Hecke–Mahler series. As a corollary, we prove that \(\rho (f_{\varvec{p}})\) is a rational number when the components of \(\varvec{p}\) are algebraic numbers.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊

Aequationes Mathematicae
MATHEMATICS, APPLIED-MATHEMATICS
CiteScore
1.70
自引率
12.50%
发文量
62
审稿时长
>12 weeks
期刊介绍:
aequationes mathematicae is an international journal of pure and applied mathematics, which emphasizes functional equations, dynamical systems, iteration theory, combinatorics, and geometry. The journal publishes research papers, reports of meetings, and bibliographies. High quality survey articles are an especially welcome feature. In addition, summaries of recent developments and research in the field are published rapidly.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


