托勒密变体的扭曲一环不变量和雅各布数
IF 1
3区 数学
Q1 MATHEMATICS
引用次数: 0
摘要
我们用托勒密坐标重新表述了扭曲一环不变量。此外,我们还证明了对于所有双曲一次穿孔环束,扭曲一环不变量等于邻接的扭曲亚历山大多项式。这表明迪莫夫特和加鲁法利迪斯提出的单环猜想对所有双曲一次穿孔环束都成立。本文章由计算机程序翻译,如有差异,请以英文原文为准。
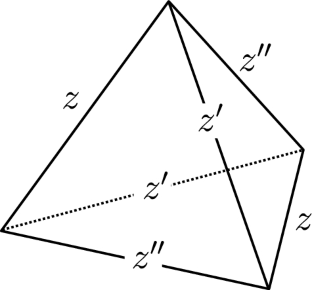
The twisted 1-loop invariant and the Jacobian of Ptolemy varieties
We reformulate the twisted 1-loop invariant in terms of Ptolemy coordinates. In addition, we prove that the twisted 1-loop invariant is equal to the adjoint twisted Alexander polynomial for all hyperbolic once-punctured torus bundles. This shows that the 1-loop conjecture proposed by Dimofte and Garoufalidis holds for all hyperbolic once-punctured torus bundles.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
1.60
自引率
0.00%
发文量
236
审稿时长
3-6 weeks
期刊介绍:
"Mathematische Zeitschrift" is devoted to pure and applied mathematics. Reviews, problems etc. will not be published.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


