关于闵科夫斯基空间中的博尔苏克问题的说明

IF 0.5 4区数学 Q3 MATHEMATICS

Doklady Mathematics Pub Date : 2024-04-18 DOI:10.1134/S1064562424701849

A. M. Raigorodskii, A. Sagdeev

{"title":"关于闵科夫斯基空间中的博尔苏克问题的说明","authors":"A. M. Raigorodskii, A. Sagdeev","doi":"10.1134/S1064562424701849","DOIUrl":null,"url":null,"abstract":"In 1993, Kahn and Kalai famously constructed a sequence of finite sets in d-dimensional Euclidean spaces that cannot be partitioned into less than \\({{(1.203 \\ldots + o(1))}^{{\\sqrt d }}}\\) parts of smaller diameter. Their method works not only for the Euclidean, but for all \\({{\\ell }_{p}}\\)-spaces as well. In this short note, we observe that the larger the value of p, the stronger this construction becomes.","PeriodicalId":531,"journal":{"name":"Doklady Mathematics","volume":"109 1","pages":"80 - 83"},"PeriodicalIF":0.5000,"publicationDate":"2024-04-18","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":"{\"title\":\"A Note on Borsuk’s Problem in Minkowski Spaces\",\"authors\":\"A. M. Raigorodskii, A. Sagdeev\",\"doi\":\"10.1134/S1064562424701849\",\"DOIUrl\":null,\"url\":null,\"abstract\":\"In 1993, Kahn and Kalai famously constructed a sequence of finite sets in d-dimensional Euclidean spaces that cannot be partitioned into less than \\\\({{(1.203 \\\\ldots + o(1))}^{{\\\\sqrt d }}}\\\\) parts of smaller diameter. Their method works not only for the Euclidean, but for all \\\\({{\\\\ell }_{p}}\\\\)-spaces as well. In this short note, we observe that the larger the value of p, the stronger this construction becomes.\",\"PeriodicalId\":531,\"journal\":{\"name\":\"Doklady Mathematics\",\"volume\":\"109 1\",\"pages\":\"80 - 83\"},\"PeriodicalIF\":0.5000,\"publicationDate\":\"2024-04-18\",\"publicationTypes\":\"Journal Article\",\"fieldsOfStudy\":null,\"isOpenAccess\":false,\"openAccessPdf\":\"\",\"citationCount\":\"0\",\"resultStr\":null,\"platform\":\"Semanticscholar\",\"paperid\":null,\"PeriodicalName\":\"Doklady Mathematics\",\"FirstCategoryId\":\"100\",\"ListUrlMain\":\"https://link.springer.com/article/10.1134/S1064562424701849\",\"RegionNum\":4,\"RegionCategory\":\"数学\",\"ArticlePicture\":[],\"TitleCN\":null,\"AbstractTextCN\":null,\"PMCID\":null,\"EPubDate\":\"\",\"PubModel\":\"\",\"JCR\":\"Q3\",\"JCRName\":\"MATHEMATICS\",\"Score\":null,\"Total\":0}","platform":"Semanticscholar","paperid":null,"PeriodicalName":"Doklady Mathematics","FirstCategoryId":"100","ListUrlMain":"https://link.springer.com/article/10.1134/S1064562424701849","RegionNum":4,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

摘要

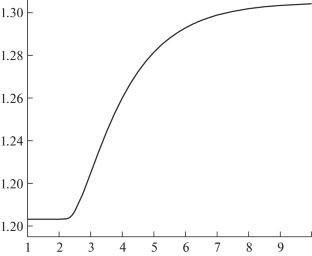
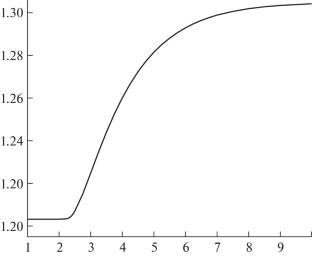
摘要1993年，卡恩和卡莱在d维欧几里得空间中构建了一个著名的有限集序列，它不能被分割成直径小于({{(1.203 \ldots + o(1))}^{{\sqrt d }}}\) 的部分。他们的方法不仅适用于欧几里得空间，也适用于所有 \({{\ell }_{p}}\)-空间。在这篇短文中，我们观察到 p 的值越大，这种构造就越强。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

A Note on Borsuk’s Problem in Minkowski Spaces

查看原文本刊更多论文

A Note on Borsuk’s Problem in Minkowski Spaces

In 1993, Kahn and Kalai famously constructed a sequence of finite sets in d-dimensional Euclidean spaces that cannot be partitioned into less than \({{(1.203 \ldots + o(1))}^{{\sqrt d }}}\) parts of smaller diameter. Their method works not only for the Euclidean, but for all \({{\ell }_{p}}\)-spaces as well. In this short note, we observe that the larger the value of p, the stronger this construction becomes.

求助全文

通过发布文献求助，成功后即可免费获取论文全文。去求助

来源期刊

Doklady Mathematics 数学-数学

CiteScore

1.00

自引率

16.70%

发文量

审稿时长

3-6 weeks

期刊介绍： Doklady Mathematics is a journal of the Presidium of the Russian Academy of Sciences. It contains English translations of papers published in Doklady Akademii Nauk (Proceedings of the Russian Academy of Sciences), which was founded in 1933 and is published 36 times a year. Doklady Mathematics includes the materials from the following areas: mathematics, mathematical physics, computer science, control theory, and computers. It publishes brief scientific reports on previously unpublished significant new research in mathematics and its applications. The main contributors to the journal are Members of the RAS, Corresponding Members of the RAS, and scientists from the former Soviet Union and other foreign countries. Among the contributors are the outstanding Russian mathematicians.